题目内容
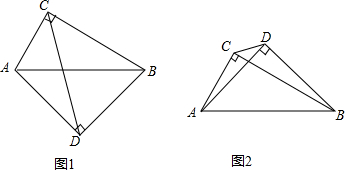
20．如果反比例函数y=$\frac{k-4}{x}$的图象位于第二、四象限内，那么满足条件的正整数k是1，2，3．分析 根据反比例函数图象所在的象限求得k-4＜0，然后得到正整数k的取值即可．
解答 解：∵反比例函数y=$\frac{k-4}{x}$的图象位于第二、四象限内，
∴k-4＜0，
则k＜4．
又k是正整数，
∴k=1，2，3．
故答案是：1，2，3．
点评 本题考查了反比例函数的图象的性质，重点是比例系数k的正负．
练习册系列答案
相关题目
11．
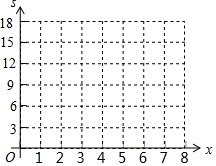某一小球以一定的初速度开始向前滚动，并且均匀减速，小球滚动的速度v（单位：米/秒）与时间x（单位：秒）之间关系的部分数据如表一：
表一：
（1）根据表一的信息，请在表二中填写滚动的距离s（单位：米）的对应值，（提示：本题中，s=$\overline{v}$×x，$\overline{v}$=$\frac{{v}_{0}+{v}_{x}}{2}$，其中，v0表示开始时的速度，vx表示x秒时的速度．）
表二：
（2）根据表二中的数据在给出的平面坐标系中画出相应的点；
（3）选择适当的函数表示s与x之间的关系，求出相应的函数解析式；
（4）当s=13.75时，求滚动时间x．
某一小球以一定的初速度开始向前滚动，并且均匀减速，小球滚动的速度v（单位：米/秒）与时间x（单位：秒）之间关系的部分数据如表一：表一：
| 时间x（秒） | 0 | 1 | 2 | 2.5 | 3 | … |
| 速度v（米/秒） | 8 | 6 | 4 | 3 | 2 | … |
表二：
| 时间x（秒） | 0 | 1 | 2 | 3 | … |
| 距离s（米） | 0 | … |
（3）选择适当的函数表示s与x之间的关系，求出相应的函数解析式；
（4）当s=13.75时，求滚动时间x．
某长方体包装盒的表面积为146cm2，其展开图如图所示．求这个包装盒的体积．
15．
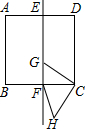如图，正方形ABCD的边长为6，EF为正方形ABCD的对称轴，交BC于F点，点G是对称轴EF上的一个动点，连接GC，将线段GC绕点C逆时针旋转90°得到HC，连接HF，则在点G运动过程中，HF的最小值是（ ）
如图，正方形ABCD的边长为6，EF为正方形ABCD的对称轴，交BC于F点，点G是对称轴EF上的一个动点，连接GC，将线段GC绕点C逆时针旋转90°得到HC，连接HF，则在点G运动过程中，HF的最小值是（ ）| A． | $\frac{1}{2}$ | B． | 2$\sqrt{2}$ | C． | 2$\sqrt{3}$ | D． | 3 |
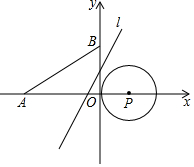如图，平面直角坐标系中，点P的坐标为（1，0），⊙P的半径为1，点A的坐标为（-3，0），点B在y轴的正半轴上，且OB=$\sqrt{3}$．若直线1：y=$\sqrt{3}$x+m从点B开始沿y轴向下平移，线段AB与线段A′B′关于直线1对称．若线段A′B′与⊙P只有一个公共点，则m的值为$\sqrt{3}$或-$\frac{\sqrt{3}}{3}$．
12．已知x=-1，y=2是二元一次方程组3x+2y=m，nx-y=1的解，则m-n的值是（ ）
| A． | 0 | B． | -2 | C． | 1 | D． | 4 |
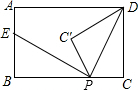如图，在矩形ABCD中，AB=3，BC=5，点P是BC边上的一个动点（点P不与点B、C重合），现将△PCD沿直线PD折叠，使点C落在点C’处，作么BPC'的角平分线交AB于点E．设BP=x，BE=y，给出如下结论：