题目内容
10.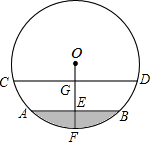 一根圆管的横截面积如图所示,圆管内原有积水的水面宽AB=40cm,水深EF=10cm,当水面上升10cm(即EG=10cm)时,水面的宽CD是多少(结果保留小数点后一位)
一根圆管的横截面积如图所示,圆管内原有积水的水面宽AB=40cm,水深EF=10cm,当水面上升10cm(即EG=10cm)时,水面的宽CD是多少(结果保留小数点后一位)
分析 连接OA、OC.设⊙O的半径是R,则OE=R-10,OG=R-20.根据垂径定理,得AE=20cm.在直角△AOE中,根据勾股定理求得R的值,再进一步在直角△COG中,根据勾股定理求得CG的长,从而再根据垂径定理即可求得CD的长.
解答  解:如图所示,连接OA、OC.
解:如图所示,连接OA、OC.
设⊙O的半径是R,则OE=R-10,OG=R-20.
∵OH⊥AB,
∴AE=$\frac{1}{2}$AB=20cm.
在直角△AOE中,根据勾股定理,得
R2=202+(R-1O)2,
解得R=25(cm).
∴OG=25-20=5,
在直角△COG中,根据勾股定理,得
CG=$\sqrt{{R}^{2}-O{G}^{2}}$=$\sqrt{2{5}^{2}-{5}^{2}}$=10$\sqrt{6}$cm.
根据垂径定理,得CD=2CG=20$\sqrt{6}$cm.
故此时水面CD的宽是20$\sqrt{6}$cm.
点评 此题综合考查了勾股定理和垂径定理的应用.垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题.

练习册系列答案
相关题目
18.已知函数y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+1.
(1)用配方法求抛物线的对称轴和顶点坐标;
(2)画出所给函数的图象;
(3)观察图象,指出当y≤0时,x的取值范围.
(1)用配方法求抛物线的对称轴和顶点坐标;
(2)画出所给函数的图象;
(3)观察图象,指出当y≤0时,x的取值范围.
15.已知,二次函数f(x)=ax2+bx+c的部分对应值如下表,则f(-2)=5.
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 0 | -3 | -4 | -3 | 0 | 5 | 12 |
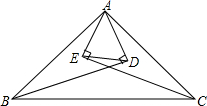 如图,△ABC中,BD,CE分别是∠ABC,∠ACB的平分线,AD⊥BD于D,AE⊥CE于E.已知AB=6,BC=7,AC=5,求DE的长.
如图,△ABC中,BD,CE分别是∠ABC,∠ACB的平分线,AD⊥BD于D,AE⊥CE于E.已知AB=6,BC=7,AC=5,求DE的长. 如图,⊙0的半径为10cm.M是弦AB上的-个动点.且线段0M长度的最小值为8cm.则弦AB=12cm.
如图,⊙0的半径为10cm.M是弦AB上的-个动点.且线段0M长度的最小值为8cm.则弦AB=12cm. 菱形ABCD中,AB=6,∠BAC=45°,M为AB上一定点(AM),N,P分别为BC、AC上的动点,则MP+NP的最小值为6.
菱形ABCD中,AB=6,∠BAC=45°,M为AB上一定点(AM),N,P分别为BC、AC上的动点,则MP+NP的最小值为6.