题目内容
13.如图,已知:△ABC与△A′B′C′中,AD、A′D′分别是BC、B′C′上的中线,CE、C′E′分别平分∠ACB,∠A′C′B′,∠ACB=∠A′C′B′,$\frac{CE}{{C}^{'}{E}^{'}}$=$\frac{BC}{{B}^{'}{C}^{'}}$,求证:$\frac{AD}{{A}^{'}{D}^{'}}$=$\frac{CE}{{C}^{'}{E}^{'}}$.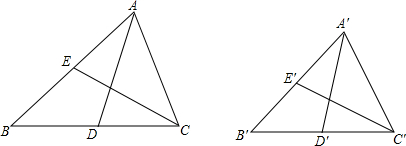
分析 根据角平分线的定义得到∠BCE=∠B′C′E′,于是推出△BCE∽△B′C′E′,得到∠B=∠B′,推出△ABC∽△A′B′C′,根据相似三角形的性质得到$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$,由AD、A′D′分别是BC、B′C′上的中线,得到BD=$\frac{1}{2}$BC,B′D′=$\frac{1}{2}$B′C′,求得$\frac{AB}{A′B′}$=$\frac{BD}{B′C′}$,推出△ABD∽△A′B′D′,得到$\frac{AD}{A′D′}=\frac{BD}{B′D′}$,通过等量代换即可得到结论.
解答 证明:∵CE、C′E′分别平分∠ACB,∠A′C′B′,∠ACB=∠A′C′B′,
∴∠BCE=∠B′C′E′,
∵$\frac{CE}{{C}^{'}{E}^{'}}$=$\frac{BC}{{B}^{'}{C}^{'}}$,
∴△BCE∽△B′C′E′,
∴∠B=∠B′,
∴△ABC∽△A′B′C′,
∴$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$,
∵AD、A′D′分别是BC、B′C′上的中线,
∴BD=$\frac{1}{2}$BC,B′D′=$\frac{1}{2}$B′C′,
∴$\frac{AB}{A′B′}$=$\frac{BD}{B′C′}$,
∴△ABD∽△A′B′D′,
∴$\frac{AD}{A′D′}=\frac{BD}{B′D′}$,
∴$\frac{AD}{A′D′}$=$\frac{\frac{1}{2}BC}{\frac{1}{2}B′C′}$=$\frac{BC}{B′C′}$,
∴$\frac{AD}{{A}^{'}{D}^{'}}$=$\frac{CE}{{C}^{'}{E}^{'}}$.
点评 本题考查了相似三角形的判定和性质,三角形的中线的定义,三角形角平分线的定义,熟练掌握相似三角形的判定和性质是解题的关键.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案| A. | 1 | B. | -1995 | C. | 1996 | D. | 1997 |
| A. | 6 | B. | 10 | C. | 12 | D. | 6或10或12 |
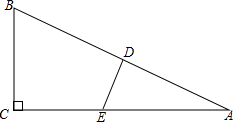 如图所示,在△ABC中,∠C=90°,∠A=30°,DE⊥AB,交AB于D,交AC于E,且CE=DE,那么DE是AB的垂直平分线吗?如果是,请加以证明;如果不是,请说明理由.
如图所示,在△ABC中,∠C=90°,∠A=30°,DE⊥AB,交AB于D,交AC于E,且CE=DE,那么DE是AB的垂直平分线吗?如果是,请加以证明;如果不是,请说明理由.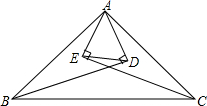 如图,△ABC中,BD,CE分别是∠ABC,∠ACB的平分线,AD⊥BD于D,AE⊥CE于E.已知AB=6,BC=7,AC=5,求DE的长.
如图,△ABC中,BD,CE分别是∠ABC,∠ACB的平分线,AD⊥BD于D,AE⊥CE于E.已知AB=6,BC=7,AC=5,求DE的长.