题目内容
11.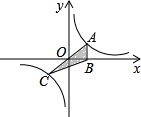 正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连结BC,若△ABC的面积为S,则( )
正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连结BC,若△ABC的面积为S,则( )| A. | S=1 | B. | S=2 | C. | S=3 | D. | S=4 |
分析 设点A坐标(x,x),根据点A,C关于原点对称,可得出点C坐标,再根据三角形的面积计算即可.
解答 解:设点A坐标(x,x),
∴点C坐标(-x,-x),
∵AB⊥x轴,
∴S△ABC=$\frac{1}{2}$AB•(0B+x)=$\frac{1}{2}$×kx×2x=x2,
∵正比例函数y=kx与反比例函数y=$\frac{1}{x}$图象相交于点A、C,
∴x2=1,
∴S△ABC=1.
故选A.
点评 本题考查了一次函数与反比例函数的交点问题,三角形的面积,解方程组等知识点,主要考查学生的计算能力,题目比较好.

练习册系列答案
相关题目
20.若A(-5,y1),B(-3,y2),C(0,y3)为二次函数y=x2+4x-5的图象上的三点,则y1、y2、y3的大小关系是( )
| A. | y2<y3<y1 | B. | y1<y2<y3 | C. | y3<y1<y2 | D. | y1<y3<y2 |
 如图,AC与BD交于点E,点E在BC的垂直平分线上.
如图,AC与BD交于点E,点E在BC的垂直平分线上.