题目内容
7.在等式x+y=12中,已知x、y均为自然数,试求x、y同时为正整数的频率$\frac{11}{13}$.分析 先求出满足x+y=12的自然数解一共有13组,再找出其中x、y同时为正整数的组数,进而求解即可.
解答 解:x、y均为自然数且x+y=12,那此二元一次方程的解为:
x=0,y=12;
或x=1,y=11;
或x=2,y=10;
或…
或x=9,y=3;
或x=10,y=2;
或x=11,y=1;
或x=12,y=0;
一共有13组解,其中有11组是x,y同为正整数的解,
那么,频率为$\frac{11}{13}$.
故答案为$\frac{11}{13}$.
点评 本题考查了频数与频率,频数是指每个对象出现的次数,频率是指每个对象出现的次数与总次数的比值(或者百分比).即频率=频数:数据总数.

练习册系列答案
相关题目
2.下列命题为真命题的是( )
| A. | 四个角相等的四边形是矩形 | B. | 对角线垂直的四边形是菱形 | ||
| C. | 对角线相等的四边形是矩形 | D. | 矩形的对角线互相垂直 |
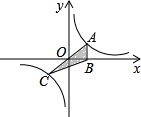 正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连结BC,若△ABC的面积为S,则( )
正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连结BC,若△ABC的面积为S,则( ) 在如图的4×4的方格内画△ABC,使它的顶点都在格点上,三条边长分别为3,4$\sqrt{\frac{1}{2}}$,$\frac{1}{5}$$\sqrt{125}$.
在如图的4×4的方格内画△ABC,使它的顶点都在格点上,三条边长分别为3,4$\sqrt{\frac{1}{2}}$,$\frac{1}{5}$$\sqrt{125}$.