题目内容
20．化简：（1）$\frac{1}{x-1}$+$\frac{2}{1-{x}^{2}}$
（2）1-$\frac{a-2}{a}$÷$\frac{{a}^{2}-4}{{a}^{2}+2a}$．
分析 （1）原式变形后，通分并利用同分母分式的减法法则计算即可得到结果；
（2）原式第二项利用除法法则变形，约分后计算即可得到结果．
解答 解：（1）原式=$\frac{x+1-2}{{x}^{2}-1}$=$\frac{x-1}{（x+1）（x-1）}$=$\frac{1}{x+1}$；
（2）原式=1-$\frac{a-2}{a}$•$\frac{a（a+2）}{（a+2）（a-2）}$=1-1=0．
点评 此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
11．
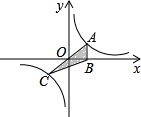正比例函数y=kx（k＞0）与反比例函数y=$\frac{1}{x}$的图象相交于A、C两点，过点A作x轴的垂线交x轴于点B，连结BC，若△ABC的面积为S，则（ ）
正比例函数y=kx（k＞0）与反比例函数y=$\frac{1}{x}$的图象相交于A、C两点，过点A作x轴的垂线交x轴于点B，连结BC，若△ABC的面积为S，则（ ）| A． | S=1 | B． | S=2 | C． | S=3 | D． | S=4 |
4．若式子$\sqrt{-a-b}$+$\frac{1}{\sqrt{ab}}$有意义，则点P（a，b）在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
11．若$\sqrt{8-n}$是整数，则正整数n的最大值是（ ）
| A． | 4 | B． | 6 | C． | 7 | D． | 8 |
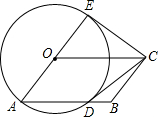如图，四边形ABCO是平行四边形，以O为圆心，OA为半径的圆交AB于D，延长AO交⊙O于点E，连接CE、CD，若CD是⊙O的切线，解答下列问题：
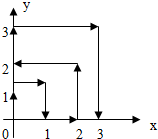一个质点在第一象限及x轴、y轴上运动，在第一秒钟，它从原点运动到（0，1），然后接着按图中箭头所示方向运动且每秒移动一个单位，那么第48秒时质点所在位置的坐标是（0，6）．