题目内容
20.若A(-5,y1),B(-3,y2),C(0,y3)为二次函数y=x2+4x-5的图象上的三点,则y1、y2、y3的大小关系是( )| A. | y2<y3<y1 | B. | y1<y2<y3 | C. | y3<y1<y2 | D. | y1<y3<y2 |
分析 先求出二次函数的对称轴,再根据二次函数的增减性以及点到对称轴的距离解答.
解答 解:二次函数的对称轴为直线x=-$\frac{4}{2×1}$=-2,
∵-2-(-5)=-2+5=3,
-2-(-3)=-2+3=1,
0-(-2)=2,
∴y2<y3<y1.
故选A.
点评 本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的增减性和对称性,确定出各点到对称轴的距离是解题的关键.

练习册系列答案
相关题目
5.已知A、B、C三点不在同一条直线上,则以这三点为顶点的平行四边形共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
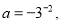
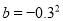 ,
, 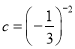 ,
, 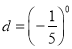 那么
那么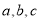 ,d三数的大小为( )
,d三数的大小为( )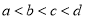 B.
B.  C.
C. 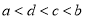 D.
D. 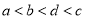
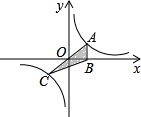 正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连结BC,若△ABC的面积为S,则( )
正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连结BC,若△ABC的面积为S,则( )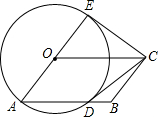 如图,四边形ABCO是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于点E,连接CE、CD,若CD是⊙O的切线,解答下列问题:
如图,四边形ABCO是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于点E,连接CE、CD,若CD是⊙O的切线,解答下列问题: