题目内容
4. 如图,AC与BD交于点E,点E在BC的垂直平分线上.
如图,AC与BD交于点E,点E在BC的垂直平分线上.(1)求证:∠EBC=∠ECB;
(2)若AE=DE,求证:△ABC≌△DCB.
分析 (1)先根据线段垂直平分线上的点到线段两端点的距离相等得出EB=EC,再根据等边对等角即可证明∠EBC=∠ECB;
(2)先利用SAS证明△AEB≌△DEC,得出∠A=∠D,由(1)得出∠ACB=∠DBC,又BC公共,根据AAS即可证明△ABC≌△DCB.
解答 证明:(1)∵点E在BC的垂直平分线上,
∴EB=EC,
∴∠EBC=∠ECB;
(2)在△AEB与△DEC中,
$\left\{\begin{array}{l}{AE=DE}\\{∠AEB=∠DEC}\\{EB=EC}\end{array}\right.$,
∴△AEB≌△DEC,
∴∠A=∠D.
在△ABC与△DCB中,
$\left\{\begin{array}{l}{∠A=∠D}\\{∠ACB=∠DBC}\\{BC=CB}\end{array}\right.$,
∴△ABC≌△DCB.
点评 本题考查了全等三角形的判定与性质,线段垂直平分线的性质,等腰三角形的性质,关键是掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL.

练习册系列答案
相关题目
15.若x<1,且y=$\frac{\sqrt{(x-1)^{2}}}{x-1}$+3,则y•$\sqrt{3y}$÷$\sqrt{\frac{1}{{y}^{4}}}$•$\sqrt{\frac{1}{y}}$的值为( )
| A. | $\frac{1}{2}\sqrt{3}$ | B. | 16$\sqrt{3}$ | C. | 64$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
11.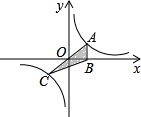 正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连结BC,若△ABC的面积为S,则( )
正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连结BC,若△ABC的面积为S,则( )
 正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连结BC,若△ABC的面积为S,则( )
正比例函数y=kx(k>0)与反比例函数y=$\frac{1}{x}$的图象相交于A、C两点,过点A作x轴的垂线交x轴于点B,连结BC,若△ABC的面积为S,则( )| A. | S=1 | B. | S=2 | C. | S=3 | D. | S=4 |
11.若$\sqrt{8-n}$是整数,则正整数n的最大值是( )
| A. | 4 | B. | 6 | C. | 7 | D. | 8 |
 如图,AC=BD,BC=AD,求证:△ABC≌△BAD.
如图,AC=BD,BC=AD,求证:△ABC≌△BAD.
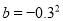 ,
, 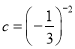 ,
, 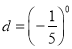 那么
那么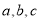 ,d三数的大小为( )
,d三数的大小为( )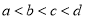 B.
B.  C.
C. 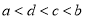 D.
D.