题目内容
现有球迷150人欲同时租用A,B,C三种型号客车去观看世界杯足球赛,其中A,B,C三种型号客车载容量分别为50人,30人,10人,要求每辆车必须满载,其中A型客车最多租两辆,则球迷们一次性到达赛场的租车方案有( )
A. 3种 B. 4种 C. 5种 D. 6种
 B
【解析】此题首先注意租用A型号客车时分两种情况讨论,进而列出方程,再进一步根据车辆数是整数进行分析.
【解析】
设B、C两种车分别租a辆、b辆.
①当A型号租用1辆时,则有
30a+10b=150﹣50,
3a+b=10.
又a,b是整数,
则a=1,b=7或a=2,b=4或a=3,b=1.
②当A型号租用2辆时,则有
30a+10b=1...
B
【解析】此题首先注意租用A型号客车时分两种情况讨论,进而列出方程,再进一步根据车辆数是整数进行分析.
【解析】
设B、C两种车分别租a辆、b辆.
①当A型号租用1辆时,则有
30a+10b=150﹣50,
3a+b=10.
又a,b是整数,
则a=1,b=7或a=2,b=4或a=3,b=1.
②当A型号租用2辆时,则有
30a+10b=1...
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案下列每一个不透明袋子中都装有若干个红球和白球(除颜色外其他均相同).
第一个袋子:红球1个,白球1个;
第二个袋子:红球1个,白球2个;
第三个袋子:红球2个,白球3个;
第四个袋子:红球4个,白球10个.
分别从中任意摸出一个球,摸到红球的可能性最大的是( )
A. 第一个袋子 B. 第二个袋子
C. 第三个袋子 D. 第四个袋子
 A
【解析】要求可能性的大小,只需求出各自所占的比例大小即可.求比例时,应注意记清各自的数目.
【解析】
第一个袋子摸到红球的可能性=;
第二个袋子摸到红球的可能性=;
第三个袋子摸到红球的可能性=;
第四个袋子摸到红球的可能性==.
故选A.
A
【解析】要求可能性的大小,只需求出各自所占的比例大小即可.求比例时,应注意记清各自的数目.
【解析】
第一个袋子摸到红球的可能性=;
第二个袋子摸到红球的可能性=;
第三个袋子摸到红球的可能性=;
第四个袋子摸到红球的可能性==.
故选A. 分式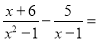 ____________
____________
 【解析】试题分析:原式=
=
=
=.
故答案为: .
【解析】试题分析:原式=
=
=
=.
故答案为: . 计算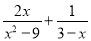 的结果是( )
的结果是( )
A. 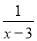 B.
B. 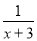 C.
C. 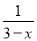 D.
D. 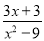
 B
【解析】原式=?===.
故选:B.
B
【解析】原式=?===.
故选:B. 如图,用锤子以相同的力将铁钉垂直钉入木块,随着铁钉的深入,铁钉所受的阻力也越来越大.当铁钉未进入木块部分长度足够时,每次钉入木块的铁钉长度是前一次的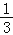 ,已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是a(cm),若铁钉总长度为6(cm),则a的取值范围是__.
,已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后,铁钉进入木块的长度是a(cm),若铁钉总长度为6(cm),则a的取值范围是__.

 ≤a<
【解析】【解析】
∵每次钉入木块的钉子长度是前一次的.已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后铁钉进入木块的长度是a(cm),
根据题意得:敲击2次后铁钉进入木块的长度是a+a=a(cm),
而此时还要敲击1次,∵铁钉总长度为6cm,故a<6,
第三次敲击进去最大长度是前一次的,也就是第二次的=a(cm),
∴ ,
∴a的取值...
≤a<
【解析】【解析】
∵每次钉入木块的钉子长度是前一次的.已知这个铁钉被敲击3次后全部进入木块(木块足够厚),且第一次敲击后铁钉进入木块的长度是a(cm),
根据题意得:敲击2次后铁钉进入木块的长度是a+a=a(cm),
而此时还要敲击1次,∵铁钉总长度为6cm,故a<6,
第三次敲击进去最大长度是前一次的,也就是第二次的=a(cm),
∴ ,
∴a的取值... 图1中所示程序进行计算:(1)若输入-3,求y的值;(2)若第一次输入x,输出的结果记为y1,第二次输入(1-x),计算的结果记为y2,要使y1>y2,你怎样选择x的值,并把x值的范围在图2中的数轴上表示出来.

 (1)-8;(2)x>0.5.
【解析】【试题分析】(1)设输入的数为x,则输出的结果y=2(x-1),当x=-3时,y=-8;
(2)y1=2(x-1);y2=-2x,又根据y1>y2,得到2(x-1)>-2x,解不等式得x>0.5,画数轴见解析.
【试题解析】
(1)y=(x-1)·2=2(x-1),当x=-3时,y=2×(-3-1)=-8;
(2)由题意知y1=...
(1)-8;(2)x>0.5.
【解析】【试题分析】(1)设输入的数为x,则输出的结果y=2(x-1),当x=-3时,y=-8;
(2)y1=2(x-1);y2=-2x,又根据y1>y2,得到2(x-1)>-2x,解不等式得x>0.5,画数轴见解析.
【试题解析】
(1)y=(x-1)·2=2(x-1),当x=-3时,y=2×(-3-1)=-8;
(2)由题意知y1=... 不等式3x+2<2x+3的解集在数轴上表示正确的是( )
A.  B.
B. 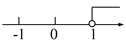 C.
C. 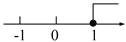 D.
D. 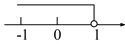
 D
【解析】【解析】
3x+2<2x+3
移项及合并同类项,得
x<1,故选D.
D
【解析】【解析】
3x+2<2x+3
移项及合并同类项,得
x<1,故选D. “二广”高速在益阳境内的建设正在紧张地进行,现有大量的沙石需要运输.“益安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.
(1)求“益安”车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,“益安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.
 【解析】
(1)设“益安”车队载重量为8吨、10吨的卡车分别有x辆、y辆,
根据题意得: ,解得: 。
答:“益安”车队载重量为8吨的卡车有5辆,10吨的卡车有7辆。
(2)设载重量为8吨的卡车增加了z辆,
依题意得:8(5+z)+10(7+6﹣z)>165,解得:z<。
∵z≥0且为整数,∴z=0,1,2,6﹣z=6,5,4。
∴车队共有3种购车方案:
...
【解析】
(1)设“益安”车队载重量为8吨、10吨的卡车分别有x辆、y辆,
根据题意得: ,解得: 。
答:“益安”车队载重量为8吨的卡车有5辆,10吨的卡车有7辆。
(2)设载重量为8吨的卡车增加了z辆,
依题意得:8(5+z)+10(7+6﹣z)>165,解得:z<。
∵z≥0且为整数,∴z=0,1,2,6﹣z=6,5,4。
∴车队共有3种购车方案:
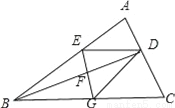
... 如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2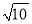 ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
 (1)四边形EBGD是菱形,理由见解析;(2).
【解析】试题分析:(1)四边形EBGD是菱形,根据已知条件易证△EFD≌△GFB,可得ED=BG,所以BE=ED=DG=GB,即可判定四边形EBGD是菱形.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:...
(1)四边形EBGD是菱形,理由见解析;(2).
【解析】试题分析:(1)四边形EBGD是菱形,根据已知条件易证△EFD≌△GFB,可得ED=BG,所以BE=ED=DG=GB,即可判定四边形EBGD是菱形.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:... 
