题目内容
下列每一个不透明袋子中都装有若干个红球和白球(除颜色外其他均相同).
第一个袋子:红球1个,白球1个;
第二个袋子:红球1个,白球2个;
第三个袋子:红球2个,白球3个;
第四个袋子:红球4个,白球10个.
分别从中任意摸出一个球,摸到红球的可能性最大的是( )
A. 第一个袋子 B. 第二个袋子
C. 第三个袋子 D. 第四个袋子
 A
【解析】要求可能性的大小,只需求出各自所占的比例大小即可.求比例时,应注意记清各自的数目.
【解析】
第一个袋子摸到红球的可能性=;
第二个袋子摸到红球的可能性=;
第三个袋子摸到红球的可能性=;
第四个袋子摸到红球的可能性==.
故选A.
A
【解析】要求可能性的大小,只需求出各自所占的比例大小即可.求比例时,应注意记清各自的数目.
【解析】
第一个袋子摸到红球的可能性=;
第二个袋子摸到红球的可能性=;
第三个袋子摸到红球的可能性=;
第四个袋子摸到红球的可能性==.
故选A.
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案下列说法正确的有( )个
①有一个外角是120°的等腰三角形是等边三角形.
②有两个外角相等的等腰三角形是等边三角形.
③有一边上的高也是这边上的中线的等腰三角形是等边三角形.
④三个外角都相等的三角形是等边三角形.
A. 4个 B. 3个 C. 2个 D. 1个
 C
【解析】利用等腰三角形和等边三角形的性质及判定即可得出答案.
【解析】
①有一个外角是120°则其相邻的内角为60°,又是等腰三角形,所以必定是等边三角形,正确;
②有两个外角相等,则与这两个外角相邻的内角也相等,但是如果这两个内角就是原来等腰三角形的两个底角,则不能判定是等边三角形;故错误;
③有一边上的高也是这边上的中线,如果这条边恰好是原等腰三角形的底边,则不能...
C
【解析】利用等腰三角形和等边三角形的性质及判定即可得出答案.
【解析】
①有一个外角是120°则其相邻的内角为60°,又是等腰三角形,所以必定是等边三角形,正确;
②有两个外角相等,则与这两个外角相邻的内角也相等,但是如果这两个内角就是原来等腰三角形的两个底角,则不能判定是等边三角形;故错误;
③有一边上的高也是这边上的中线,如果这条边恰好是原等腰三角形的底边,则不能... 我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:
(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;
(2)探究:当等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和与其中一条对角线的大小关系,并证明你的结论.
 (1)梯形、矩形、正方形;(2)答案见解析
【解析】试题分析:(1)等腰梯形、矩形、正方形,任选两个即可;
(2)等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和大于或等于一条对角线的长.分两种情况证明:当BC与CE不在同一条直线上时,60°角所对的两边之和大于其中一条对角线的长;当BC与CE在同一条直线上时60°角所对的两边之和等于其中一条对角线的长.
...
(1)梯形、矩形、正方形;(2)答案见解析
【解析】试题分析:(1)等腰梯形、矩形、正方形,任选两个即可;
(2)等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和大于或等于一条对角线的长.分两种情况证明:当BC与CE不在同一条直线上时,60°角所对的两边之和大于其中一条对角线的长;当BC与CE在同一条直线上时60°角所对的两边之和等于其中一条对角线的长.
... 下列选项中的四边形只有一个为平行四边形,根据图中所给的边长长度及角度,判断哪一个为平行四边形?( )
A. 
B. 
C. 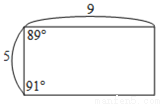
D. 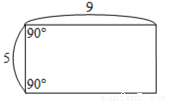
 B
【解析】解:A.上、下这一组对边平行,可能为等腰梯形;
B.上、下这一组对边平行,可能为等腰梯形,但此等腰梯形底角为90°,所以为平行
四边形;
C.上、下这一组对边平行,可能为梯形;
D.上、下这一组对边平行,可能为梯形;
故选B.
B
【解析】解:A.上、下这一组对边平行,可能为等腰梯形;
B.上、下这一组对边平行,可能为等腰梯形,但此等腰梯形底角为90°,所以为平行
四边形;
C.上、下这一组对边平行,可能为梯形;
D.上、下这一组对边平行,可能为梯形;
故选B. 小明每天早上要在7:50之前赶到距家1 000 m的学校上学.一天早上,小明以80 m/min的速度出发去上学.5 min后,小明的爸爸发现小明忘了带数学书,于是,爸爸立即以100 m/min的速度去追赶小明,结果在途中追上了小明.试探究这个事件是什么事件.
 不可能事件
【解析】试题分析:根据题目所给题设条件可知,这是考查一元一次方程的应用问题,关键在于弄清题意,找出等量关系即:小明爸爸和小明所行路程相等,列出方程求解.
解:是不可能事件.理由如下:
设小明的爸爸用x min追上小明,则可列方程
80(x+5)=100x,解得x=20.此时80(x+5)=80×(20+5)=2 000>1 000,说明这时小明已经到学校了,故小...
不可能事件
【解析】试题分析:根据题目所给题设条件可知,这是考查一元一次方程的应用问题,关键在于弄清题意,找出等量关系即:小明爸爸和小明所行路程相等,列出方程求解.
解:是不可能事件.理由如下:
设小明的爸爸用x min追上小明,则可列方程
80(x+5)=100x,解得x=20.此时80(x+5)=80×(20+5)=2 000>1 000,说明这时小明已经到学校了,故小... 一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )
A. 至少有1个球是黑球
B. 至少有1个球是白球
C. 至少有2个球是黑球
D. 至少有2个球是白球
 A
【解析】试题分析:根据必然事件、不可能事件、随机事件的概念进行判断即可.
至少有1个球是黑球是必然事件,A正确;
至少有1个球是白球是随机事件,B错误;
至少有2个球是黑球是随机事件,C错误;
至少有2个球是白球是随机事件,D错误,
故选:A.
A
【解析】试题分析:根据必然事件、不可能事件、随机事件的概念进行判断即可.
至少有1个球是黑球是必然事件,A正确;
至少有1个球是白球是随机事件,B错误;
至少有2个球是黑球是随机事件,C错误;
至少有2个球是白球是随机事件,D错误,
故选:A. 计算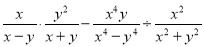
 【解析】试题分析:分式乘除法和减法的混合运算应根据运算顺序先算乘除后算加减.
试题解析:
原式=
【解析】试题分析:分式乘除法和减法的混合运算应根据运算顺序先算乘除后算加减.
试题解析:
原式= 计算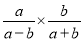 等于( )
等于( )
A. 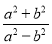 B.
B. 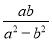 C.
C. 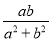 D.
D. 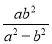
 B
【解析】试题解析: ,故答案是B选项
故选B.
B
【解析】试题解析: ,故答案是B选项
故选B. 现有球迷150人欲同时租用A,B,C三种型号客车去观看世界杯足球赛,其中A,B,C三种型号客车载容量分别为50人,30人,10人,要求每辆车必须满载,其中A型客车最多租两辆,则球迷们一次性到达赛场的租车方案有( )
A. 3种 B. 4种 C. 5种 D. 6种
 B
【解析】此题首先注意租用A型号客车时分两种情况讨论,进而列出方程,再进一步根据车辆数是整数进行分析.
【解析】
设B、C两种车分别租a辆、b辆.
①当A型号租用1辆时,则有
30a+10b=150﹣50,
3a+b=10.
又a,b是整数,
则a=1,b=7或a=2,b=4或a=3,b=1.
②当A型号租用2辆时,则有
30a+10b=1...
B
【解析】此题首先注意租用A型号客车时分两种情况讨论,进而列出方程,再进一步根据车辆数是整数进行分析.
【解析】
设B、C两种车分别租a辆、b辆.
①当A型号租用1辆时,则有
30a+10b=150﹣50,
3a+b=10.
又a,b是整数,
则a=1,b=7或a=2,b=4或a=3,b=1.
②当A型号租用2辆时,则有
30a+10b=1... 
