题目内容
3.先化简,再求值:($\frac{a}{{a}^{2}-{b}^{2}}$-$\frac{1}{a+b}$)÷$\frac{b}{b-a}$,其中a=1,b=2.分析 首先根据分式混合运算的运算顺序,先计算小括号里面的,再计算除法,把原式进行化简,然后把a=1,b=2代入化简后的算式,求出算式($\frac{a}{{a}^{2}-{b}^{2}}$-$\frac{1}{a+b}$)÷$\frac{b}{b-a}$的值是多少即可.
解答 解:($\frac{a}{{a}^{2}-{b}^{2}}$-$\frac{1}{a+b}$)÷$\frac{b}{b-a}$
=($\frac{a}{{a}^{2}-{b}^{2}}$-$\frac{a-b}{{a}^{2}{-b}^{2}}$)÷$\frac{b}{b-a}$
=$\frac{b}{{a}^{2}{-b}^{2}}÷\frac{b}{b-a}$
=-$\frac{1}{a+b}$,
当a=1,b=2时,
-$\frac{1}{a+b}$=-$\frac{1}{1+2}=-\frac{1}{3}$.
点评 此题主要考查了分式的化简求值问题,注意化简时不能跨度太大,而缺少必要的步骤,解答此题的关键是要明确:代入求值时,有直接代入法,整体代入法等常用方法.解题时可根据题目的具体条件选择合适的方法.当未知数的值没有明确给出时,所选取的未知数的值必须使原式中的各分式都有意义,且除数不能为0.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15.下列图案中既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.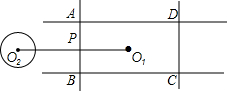 如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
 如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )
如图,矩形ABCD的长为20,宽为14,点O1为矩形的中心,⊙O2的半径为5,O1O2⊥AB于点P,O1O2=23.若⊙O2绕点P按顺时针方向旋转360°,在旋转过程中,⊙O2与矩形的边所在的直线相切的位置一共出现( )| A. | 18次 | B. | 12次 | C. | 8次 | D. | 4次 |
15.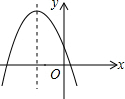 抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )
抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )
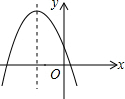 抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )
抛物线y=ax2+bx+c(a≠0)大致图象如图所示,则双曲线y=$\frac{b}{ax}$图象在( )| A. | 一、三象限 | B. | 一、二象限 | C. | 二、三象限 | D. | 二、四象限 |
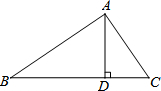 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,AB=8,AC=6.求AD的长.
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,AB=8,AC=6.求AD的长.