题目内容
18.如图,∠B和∠D的两边分别平行.(1)在图1 中,∠B和∠D的数量关系是∠B=∠D,在图2中,∠B和∠D的数量关系是∠B+∠D=180°;
(2)用一句话归纳的命题为:如果两个角的两边分别平行,则这两个角相等或互补;并请选择图1或图2中一种情况说明理由;
(3)应用:若两个角的两边分别互相平行,其中一个角是另一个角的2倍,求这两个角的度数.
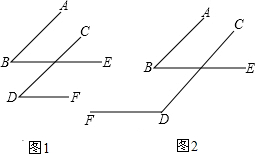
分析 (1)在图1中,首先根据AB∥CD,可得∠B=∠1;然后根据BE∥DF,可得∠1=∠D,所以∠B=∠D,据此判断即可.
在图2中,首先根据AB∥CD,可得∠B=∠1,然后根据BE∥DF,判断∠2+∠D=180°,即可判断出∠B+∠D=180°.
(2)首先判断出用一句话归纳的命题为:如果两个角的两边分别平行,则这两个角相等或互补;然后选择图1中的情况加以说明即可.
(3)若两个角的两边分别互相平行,其中一个角是另一个角的2倍,再根据这两个角互补,求出这两个角的度数各是多少即可.
解答 解:(1)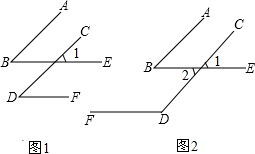 ,
,
在图1中,
∵AB∥CD,
∴∠B=∠1,
∵BE∥DF,
∴∠1=∠D,
∴∠B=∠D.
在图2中,
∵AB∥CD,
∴∠B=∠1,
∵BE∥DF,
∴∠2+∠D=180°,
又∵∠1=∠2,
∴∠1+∠D=180°,
∴∠B+∠D=180°.
(2)用一句话归纳的命题为:
如果两个角的两边分别平行,则这两个角相等或互补;
例如在图1中,
∵AB∥CD,
∴∠B=∠1,
∵BE∥DF,
∴∠1=∠D,
∴∠B=∠D.
(3)如果两个角的两边分别平行,则这两个角相等或互补,
∵其中一个角是另一个角的2倍,
∴较小的角的度数是:
180°÷(1+2)=180°÷3=60°,
∴较大的角的度数是:
60°×2=120°,
∴这两个角的度数分别是60°、120°.
故答案为:∠B=∠D;∠B+∠D=180°;如果两个角的两边分别平行,则这两个角相等或互补.
点评 此题主要考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.③定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.

| A. | 4 | B. | $\sqrt{41}$ | C. | 4或$\sqrt{34}$ | D. | 4或$\sqrt{41}$ |
| A. | -3 | B. | 3 | C. | -7 | D. | 7 |
 如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则cosD=$\frac{1}{3}$.
如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC=2,则cosD=$\frac{1}{3}$.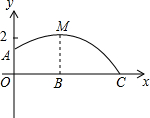 如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头部的正上方达到最高点M,距地面4米高,球落地为C点.
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头部的正上方达到最高点M,距地面4米高,球落地为C点.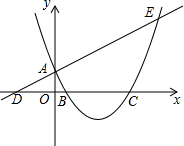 如图,已知直线y=$\frac{1}{2}$x+1与y轴交于点A,与x轴交于点D,抛物线y=$\frac{1}{2}$x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
如图,已知直线y=$\frac{1}{2}$x+1与y轴交于点A,与x轴交于点D,抛物线y=$\frac{1}{2}$x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).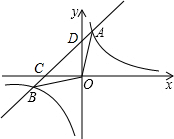 已知一次函数y1=kx+b与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.一次函数y1=kx+b与坐标轴交于C、D两点.求△AOB的面积.
已知一次函数y1=kx+b与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.一次函数y1=kx+b与坐标轴交于C、D两点.求△AOB的面积.