题目内容
11.水果批发商销售每箱进价为40元的长寿湖夏橙,市场调查发现,若以每箱60元的价格销售,平均每天销售300箱,价格每提高1元,平均每天少销售10箱.(1)求平均每天销售量y箱与销售价x之间的函数关系式;
(2)要想获得6000元的利润则长寿湖夏橙的定价应是多少?
(3)当每箱长寿湖夏橙的销售价为多少元时,可以获得最大利润?最大利润是多少?
分析 (1)平均每天销售量y=原来的销售量300-10×相对于60元的单价提高的价格;
(2)销售利润w=每箱苹果的利润×平均每天销售量;
(3)结合(2)得到的关系式,用配方法得到相应的销售价和最大利润即可
解答 解:(1)原来每箱销售价60元,价格每提高1元少销售10箱,
若售价为x,
则提高(x-60)元,
则每天少销售10(x-60)箱,
则提价后每天销售y=300-10(x-60)=-10x+900;
(2)设每件售价x元,
则每件涨价为(x-60)元,
依题意列方程 (x-40)[300-10(x-60)]=6000,
x2-130x+4200=0,
解得X1=60,X2=70.
答:要想获得6000元的利润则长寿湖夏橙的定价应是60元或70元;
(3)设每箱售价为x元时获得的总利润为W元.
w=(x-40)[300-10(x-60)]
=(x-40)(900-10x)
=-10x2+1300x-36000
=-10(x2-130x )-36000
=-10[(x-65)2-4225]-36000
=-10(x-65)2+6250,
当x=65时,y的最大值是6250.
答:定价为65元时,利润最大为6250.
点评 本题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常利用函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值).

练习册系列答案
相关题目
3.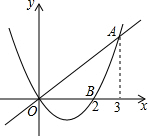 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )| A. | 0<x<2 | B. | 0<x<3 | C. | 2<x<3 | D. | x<0或x>3 |
20.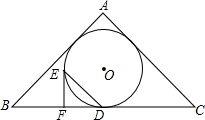 如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )
如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )
 如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )
如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
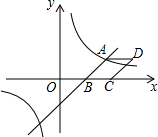 如图,已知一次函数y=$\frac{3}{2}$x-3与反比例函数y=$\frac{k}{x}$的图象相交于点A(4,n),与x轴相交于点B.
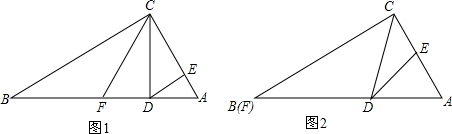
如图,已知一次函数y=$\frac{3}{2}$x-3与反比例函数y=$\frac{k}{x}$的图象相交于点A(4,n),与x轴相交于点B.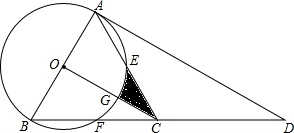 如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F
如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F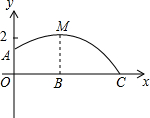 如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头部的正上方达到最高点M,距地面4米高,球落地为C点.
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头部的正上方达到最高点M,距地面4米高,球落地为C点.