题目内容
12.正比例函数y=kx的图象经过点(-2,1)、(1,y1)、(2,y2),则y1>y2(填“<”或“>”).分析 先得出正比例函数的解析式为y=-$\frac{1}{2}$x,根据k=-$\frac{1}{2}$得出y随x的增大而减小,根据2>1即可推出y1>y2.
解答 解:把点(-2,1)代入正比例函数y=kx中,
可得:y=-$\frac{1}{2}$x,
∵k=-$\frac{1}{2}$<0,
∴y随x的增大而减小,
∵2>1,
∴y1>y2.
故答案为:>.
点评 本题考查了一次函数的图象上点的坐标特征,注意:y=kx中,当k>0时,y随x的增大而增大,当k<0时,y随x的增大而减小.

练习册系列答案
相关题目
3.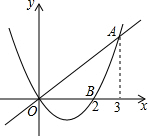 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )| A. | 0<x<2 | B. | 0<x<3 | C. | 2<x<3 | D. | x<0或x>3 |
20.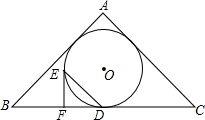 如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )
如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )
 如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )
如图,在△ABC中,AB=AC=5,BC=7,△ABC的内切圆⊙O与边BC相切于点D,过点D作DE∥AC交⊙O于点E,过点E作⊙O的切线交BC于点F,则DE-EF的值等于( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
17.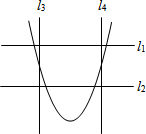 如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )
如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )
 如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )
如图,水平线l1∥l2,铅垂线l3∥l4,l1⊥l3,若选择l1、l2其中一条当成x轴,且向右为正方向,再选择l3、l4其中一条当成y轴,且向上为正方向,并在此平面直角坐标系中画出二次函数y=ax2-ax-a的图象,则下列关于x、y轴的叙述,正确的是( )| A. | l1为x轴,l3为y轴 | B. | l1为x轴,l4为y轴 | C. | l2为x轴,l3为y轴 | D. | l2为x轴,l4为y轴 |
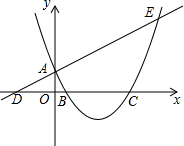 如图,已知直线y=$\frac{1}{2}$x+1与y轴交于点A,与x轴交于点D,抛物线y=$\frac{1}{2}$x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
如图,已知直线y=$\frac{1}{2}$x+1与y轴交于点A,与x轴交于点D,抛物线y=$\frac{1}{2}$x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).