题目内容
14.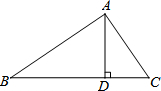 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,AB=8,AC=6.求AD的长.
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,AB=8,AC=6.求AD的长.
分析 首先利用勾股定理得出BC的长,再利用直角三角形的面积求法得出AD的长.
解答 解:∵在Rt△ABC中,∠BAC=90°,AB=8,AC=6,
∴BC=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵AD⊥BC于点D,
∴AD×BC=AB×AC,
∴AD=$\frac{AB×AC}{BC}$=$\frac{6×8}{10}$=4.8.
点评 此题主要考查了勾股定理以及三角形面积,熟练利用三角形面积求出是解题关键.

练习册系列答案
相关题目
4.在同一平面直角坐标系中,若一次函数y=-x+1与y=2x+4的图象交于点M,则点M的坐标为( )
| A. | (-1,-2) | B. | (-1,2) | C. | (2,1) | D. | (-2,1) |
9.直角三角形的两边长分别为3和5,则另一边长为( )
| A. | 4 | B. | $\sqrt{41}$ | C. | 4或$\sqrt{34}$ | D. | 4或$\sqrt{41}$ |
19.在平面直角坐标系中,抛物线y=x2-1与x轴的交点的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
6.下列关系式中,正确的是( )
| A. | (a+b)2=a2-2ab+b2 | B. | (a-b)2=a2-b2 | C. | (a+b)(-a+b)=b2-a2 | D. | (a+b)(-a-b)=a2-b2 |
3.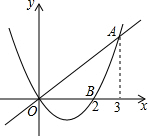 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若0<y1<y2,则x的取值范围是( )| A. | 0<x<2 | B. | 0<x<3 | C. | 2<x<3 | D. | x<0或x>3 |
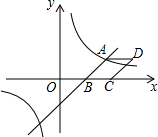 如图,已知一次函数y=$\frac{3}{2}$x-3与反比例函数y=$\frac{k}{x}$的图象相交于点A(4,n),与x轴相交于点B.
如图,已知一次函数y=$\frac{3}{2}$x-3与反比例函数y=$\frac{k}{x}$的图象相交于点A(4,n),与x轴相交于点B.