题目内容
在Rt△ABC中,∠C=90°,AB=5,三角形的面积等于6,求三角形的内切圆半径r.
考点:三角形的内切圆与内心
专题:
分析:首先运用勾股定理及三角形的面积公式列出方程组求出两条直角边的长;然后再次利用面积公式求出三角形的内切圆半径r.
解答:解:设该三角形的两直角边分别为AC=x,BC=y;
由题意得
xy=6 ①,x2+y2=25 ②;
由①×4+②得:(x+y)2=49,
故x+y=7 ③;
联立①、③并解得:x=3,y=4或x=4,y=3;
设内切圆的半径为r,则圆心到三边的距离均为r;
根据圆的面积公式:
(AB+AC+BC)•r=6,
即
(3+4+5)r=6,
解得r=1.
故三角形的内切圆半径r=1.
由题意得
| 1 |
| 2 |
由①×4+②得:(x+y)2=49,
故x+y=7 ③;
联立①、③并解得:x=3,y=4或x=4,y=3;
设内切圆的半径为r,则圆心到三边的距离均为r;
根据圆的面积公式:
| 1 |
| 2 |
即
| 1 |
| 2 |
解得r=1.
故三角形的内切圆半径r=1.
点评:该命题考查了三角形的内切圆与内心的性质及其应用问题;解题的关键是灵活运用切线的性质及勾股定理等知识点来解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列关于x的方程中,一定是一元二次方程的为( )
| A、ax2+bx+c=0 |
| B、x2_2=(x+3)2 |
| C、2x+3x-5=0 |
| D、x2=-1 |
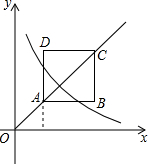 如图,正方形ABCD位于第一象限,AC=2
如图,正方形ABCD位于第一象限,AC=2| 2 |
| k |
| x |
| A、0<k≤1或k≥6 |
| B、1≤k≤6 |
| C、1≤k≤9 |
| D、0<k≤1或k≥9 |
 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,求证:
如图,Rt△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,求证: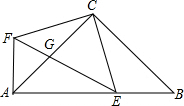 如图,在等腰Rt△ABC中,AC=BC,∠ACB=90°,点E在线段AB上,CF⊥CE,CF=CE,EF交AC于G,连接AF.
如图,在等腰Rt△ABC中,AC=BC,∠ACB=90°,点E在线段AB上,CF⊥CE,CF=CE,EF交AC于G,连接AF.