题目内容
甲、乙两商场节日举办促销活动,甲商场的优惠方案是:累计购买100商品后,再购买的商品按原价的90%收费;乙商场的优惠方案是:累计购买50元商品后,再购买的商品按原价的95%收费.小明准备购买的商品正好两家商场都有,且原价相同.
(1)如果小明累计购物不超过100元,那么小明该在哪个商场购物比较合算?
(2)如果小明累计购物超过100元,那在哪个商场购物比较合算?
(1)如果小明累计购物不超过100元,那么小明该在哪个商场购物比较合算?
(2)如果小明累计购物超过100元,那在哪个商场购物比较合算?
考点:一元一次不等式的应用
专题:
分析:(1)设购买商品的价格为x元,在甲乙两个商场实际付费为y甲元,y乙元,分别表示出y与x的函数关系式,再将两个解析式购成不等式组求出其解即可.
(2)根据(1)求出来的解析式,分类讨论,当y甲=y乙时,当y甲>y乙时,当y甲<y乙时,分别求出x取值范围就可以得出结论.
(2)根据(1)求出来的解析式,分类讨论,当y甲=y乙时,当y甲>y乙时,当y甲<y乙时,分别求出x取值范围就可以得出结论.
解答:解:设购买商品的价格为x元,在甲乙两个商场实际付费为y甲元,y乙元,由题意,得
y甲=
,
y乙=
,
当x≤50时,y甲=y乙,
当50<x≤100时,
当y甲=y乙时,
x=0.95x+2.5,
x=50(舍去),
当y甲>y乙时,
x>0.95x+2.5时,
x>50,
当y甲<y乙时,
x<50(舍去),
∴当小明购买商品的价格不超过50元时,两家一样优惠,当购买商品的价格超过50元不超过100元时在乙商场购买优惠些;
(2)由题意,得
当y甲=y乙时,
0.9x+10=0.95x+2.5,
解得:x=150,
当y甲>y乙时,
0.9x+10>0.95x+2.5,
解得:x<150;
当y甲<y乙时,
0.9x+10<0.95x+2.5,
解得:x>150.
综上所述:当x=150,两家一样优惠,当100<x<150时乙商场优惠些,当x>150时,甲商场优惠些.
y甲=
|
y乙=
|
当x≤50时,y甲=y乙,
当50<x≤100时,
当y甲=y乙时,
x=0.95x+2.5,
x=50(舍去),
当y甲>y乙时,
x>0.95x+2.5时,
x>50,
当y甲<y乙时,
x<50(舍去),
∴当小明购买商品的价格不超过50元时,两家一样优惠,当购买商品的价格超过50元不超过100元时在乙商场购买优惠些;
(2)由题意,得
当y甲=y乙时,
0.9x+10=0.95x+2.5,
解得:x=150,
当y甲>y乙时,
0.9x+10>0.95x+2.5,
解得:x<150;
当y甲<y乙时,
0.9x+10<0.95x+2.5,
解得:x>150.
综上所述:当x=150,两家一样优惠,当100<x<150时乙商场优惠些,当x>150时,甲商场优惠些.
点评:本题考查了设计方案的运用,分类讨论思想的运用,列一元一次不等式组解实际问题的运用,解答时建立函数关系式和不等式是关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
下列运算正确的是( )
A、-
| ||||||||
| B、-7-2×5=-9×5=-45 | ||||||||
C、3÷
| ||||||||
D、-
|
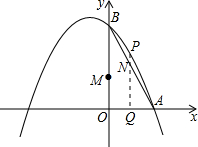 如图,抛物线的对称轴是x=-1,与x轴交于点A(1,0),与y轴交于点 B(0,3).动点Q从点O出发,以每秒1个单位长度的速度在线段OA上运动,同时动点M从O点出发以每秒3个单位长度的速度在线段OB上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒.
如图,抛物线的对称轴是x=-1,与x轴交于点A(1,0),与y轴交于点 B(0,3).动点Q从点O出发,以每秒1个单位长度的速度在线段OA上运动,同时动点M从O点出发以每秒3个单位长度的速度在线段OB上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒. 如图,正方形ABCD的边长为2,M为AD的中点,N在边CD上且∠NMB=∠MBC,MN的延长线与BC的延长线交于点G,则GN的长是
如图,正方形ABCD的边长为2,M为AD的中点,N在边CD上且∠NMB=∠MBC,MN的延长线与BC的延长线交于点G,则GN的长是 如图所示,正方形ABCD的边长是1,P为CD的中点,PQ⊥AP,交BC于Q,求BQ的长.
如图所示,正方形ABCD的边长是1,P为CD的中点,PQ⊥AP,交BC于Q,求BQ的长.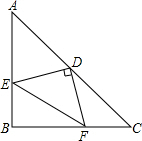 如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,过D点作DE⊥DF,交AB于E,交BC为F,
如图,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,过D点作DE⊥DF,交AB于E,交BC为F,