题目内容
13.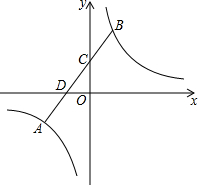 如图,点A、B分别在反比例函数y=$\frac{k}{x}$图象的两支上,连接AB交x轴于点C,交y轴于点D,则AD与BC的大小关系为( )
如图,点A、B分别在反比例函数y=$\frac{k}{x}$图象的两支上,连接AB交x轴于点C,交y轴于点D,则AD与BC的大小关系为( )| A. | AD>BC | B. | AD=BC | C. | AD<BC | D. | 无法判断 |
分析 作BN⊥x轴于N,AM⊥y轴于M,AM与BN相交于E,连结MN,如图,设A(a,$\frac{k}{a}$),B(b,$\frac{k}{b}$),则可表示出AE=b-a,EN=-$\frac{k}{a}$,BE=$\frac{k}{b}$-$\frac{k}{a}$,于是可计算出$\frac{EM}{EA}$=$\frac{EN}{EB}$=$\frac{b}{b-a}$,加上∠MEN=∠AEB,则可判断△EMN∽△EAB,所以∠EMN=∠EAB,于是可判断MN∥AB,易得四边形AMND和四边形CMNB都是平行四边形,所以MN=AD=BC.
解答  解:作BN⊥x轴于N,AM⊥y轴于M,AM与BN相交于E,连结MN,如图,设A(a,$\frac{k}{a}$),B(b,$\frac{k}{b}$),
解:作BN⊥x轴于N,AM⊥y轴于M,AM与BN相交于E,连结MN,如图,设A(a,$\frac{k}{a}$),B(b,$\frac{k}{b}$),
则AE=b-a,ME=b,EN=-$\frac{k}{a}$,BE=$\frac{k}{b}$-$\frac{k}{a}$,
∵$\frac{EM}{EA}$=$\frac{b}{b-a}$,$\frac{EN}{EB}$=$\frac{-\frac{k}{a}}{\frac{k}{b}-\frac{k}{a}}$=$\frac{b}{b-a}$,
∴$\frac{EM}{EA}$=$\frac{EN}{EB}$,
而∠MEN=∠AEB,
∴△EMN∽△EAB,
∴∠EMN=∠EAB,
∴MN∥AB,
而AM∥DN,CM∥BN,
∴四边形AMND和四边形CMNB都是平行四边形,
∴MN=AD,MN=BC,
∴AD=BC.
故选B.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了相似三角形的判定与性质和平行四边形的判定与性质.

 如图,正五边形ABCDE,B′是边BC上任意一点,以AB′为边(在BC的上方),向外作正五边形A′B′C′D′E′,连结CC′,则∠B′CC′=( )
如图,正五边形ABCDE,B′是边BC上任意一点,以AB′为边(在BC的上方),向外作正五边形A′B′C′D′E′,连结CC′,则∠B′CC′=( )| A. | 108° | B. | 126° | C. | 144° | D. | 162° |
| A. | +5 | B. | -5.25 | C. | 0 | D. | 8.3 |
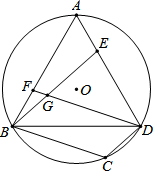 如图,已知△ABD为⊙O的内接正三角形,AB=2$\sqrt{7}$,E、F分别为边AD、AB上的动点,且AE=BF,DF与BE相交于G点,过B点作BC∥DF交$\widehat{BD}$于点C,连接CD.
如图,已知△ABD为⊙O的内接正三角形,AB=2$\sqrt{7}$,E、F分别为边AD、AB上的动点,且AE=BF,DF与BE相交于G点,过B点作BC∥DF交$\widehat{BD}$于点C,连接CD.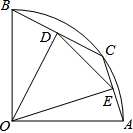 如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点,OD⊥BC,OE⊥AC,垂足分别为D、E.设BD=m,则m的取值范围是0<m<$\sqrt{2}$,.
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点,OD⊥BC,OE⊥AC,垂足分别为D、E.设BD=m,则m的取值范围是0<m<$\sqrt{2}$,.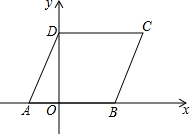 如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(-3,0),∠DAB=60°,点B、D分别在x轴、y轴上,求点C的坐标及该菱形的面积.
如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(-3,0),∠DAB=60°,点B、D分别在x轴、y轴上,求点C的坐标及该菱形的面积.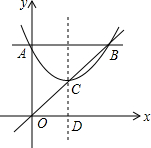 如图,抛物线y=$\frac{1}{3}$x2+bx+6与y轴相交于点A,与过点A且平行于x轴的直线相交于点B(点B在第一象限),抛物线的顶点C在直线OB上,平移直线OB,使平移后的直线OB与抛物线只有一个交点,则直线OB向右平移了$\frac{3}{4}$个单位.
如图,抛物线y=$\frac{1}{3}$x2+bx+6与y轴相交于点A,与过点A且平行于x轴的直线相交于点B(点B在第一象限),抛物线的顶点C在直线OB上,平移直线OB,使平移后的直线OB与抛物线只有一个交点,则直线OB向右平移了$\frac{3}{4}$个单位.