题目内容
3.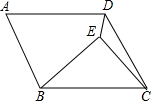 如图,在?ABCD内有一点E,如果满足∠EDA=90°,∠EBC=∠EDC,∠ECB=45°,试问是否有与BE相等的线段?
如图,在?ABCD内有一点E,如果满足∠EDA=90°,∠EBC=∠EDC,∠ECB=45°,试问是否有与BE相等的线段?
分析 延长DE与BC交于点F,由平行四边形的性质得出AD∥BC,AB=DC,得出∠DFC=∠EAD=90°=∠BFE,由AAS证明△BFE≌△DFC,得出对应边相等BE=DC,即可得出BE=AB.
解答 解:有,BE=DC,BE=AB;理由如下:
延长DE与BC交于点F,如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=DC,
∴∠DFC=∠EAD=90°,
∴∠BFE=90°,∠FEC=90°-∠ECB=45°=∠ECB,
∴∠BFE=∠DFC,FE=FC,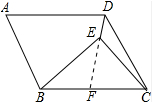 在△BFE和△DFC中,
在△BFE和△DFC中,
$\left\{\begin{array}{l}{∠EBC=∠EDC}&{\;}\\{∠BFE=∠DFC}&{\;}\\{FE=FC}&{\;}\end{array}\right.$,
∴△BFE≌△DFC(AAS),
∴BE=DC,
∴BE=AB.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质、平行线的性质;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.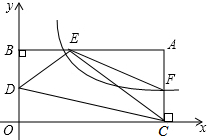 如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )
如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )
 如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )
如图,点A在直角坐标系xOy第一象限中,AB⊥y轴于点B,AC⊥x轴于点C,点D是BO的中点,反比例函数y=$\frac{k}{x}$的图象交AB于点E,交AC于点F,且满足AE=2BE.若△DEC的面积为1,则△AEF的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | 1 |
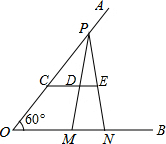 如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,点C为线段OP上任意一点,CD∥ON交PM、PN分别为D、E.若MN=3,则$\frac{CD}{DE}$的值为$\frac{7}{6}$.
如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边OB上,PM=PN,点C为线段OP上任意一点,CD∥ON交PM、PN分别为D、E.若MN=3,则$\frac{CD}{DE}$的值为$\frac{7}{6}$.
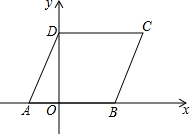 如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(-3,0),∠DAB=60°,点B、D分别在x轴、y轴上,求点C的坐标及该菱形的面积.
如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(-3,0),∠DAB=60°,点B、D分别在x轴、y轴上,求点C的坐标及该菱形的面积.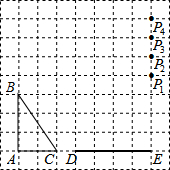 如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为P3.
如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为P3.