题目内容
7.观察下列等式:a1=n,a2=1-$\frac{1}{{a}_{{1}_{\;}}}$,a3=1-$\frac{1}{{a}_{2}}$,a4=1-$\frac{1}{{a}_{3}}$,…根据其蕴含的规律可得( )| A. | a2016=n | B. | a2016=$\frac{n-1}{n}$ | C. | a2016=$\frac{1}{n-1}$ | D. | a2016=$\frac{1}{1-n}$ |
分析 根据题意分别用含n的式子表示出a1、a2、a3、a4,从而得出数列的循环周期为3,据此即可得解答.
解答 解:∵a1=n,
a2=1-$\frac{1}{{a}_{{1}_{\;}}}$=1-$\frac{1}{n}$=$\frac{n-1}{n}$,
a3=1-$\frac{1}{{a}_{2}}$=1-$\frac{n}{n-1}$=-$\frac{1}{n-1}$,
a4=1-$\frac{1}{{a}_{3}}$=1+n-1=n,
∴这一列数每3个数为一周期,
∵2016÷3=672,
∴a2016=a3=-$\frac{1}{n-1}$=$\frac{1}{1-n}$,
故选:D.
点评 本题主要考查数字的变化规律,根据已知数列的计算公式得出其循环周期是解题的关键.

练习册系列答案
相关题目
4.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{36}$ | C. | $\sqrt{\frac{a}{b}}$ | D. | $\sqrt{a+5}$ |
5.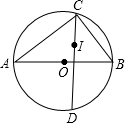 如图,在△ABC中,∠ACB=90°,AB=2,点I是△ABC的内心,CI的延长线交△ABC的外接圆⊙O于点D,则DI的长为( )
如图,在△ABC中,∠ACB=90°,AB=2,点I是△ABC的内心,CI的延长线交△ABC的外接圆⊙O于点D,则DI的长为( )
 如图,在△ABC中,∠ACB=90°,AB=2,点I是△ABC的内心,CI的延长线交△ABC的外接圆⊙O于点D,则DI的长为( )
如图,在△ABC中,∠ACB=90°,AB=2,点I是△ABC的内心,CI的延长线交△ABC的外接圆⊙O于点D,则DI的长为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 1 |
17.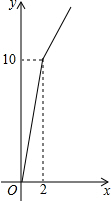 某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折.某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出函数图象.如表是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10).请你结合表格和图象:
某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折.某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出函数图象.如表是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10).请你结合表格和图象:
(1)指出付款金额和购买量哪个变量是函数的自变量x,并直接写出表中a、b的值;
(2)求出当x>2时,y关于x的函数解析式;
(3)甲农户将8.8元钱全部用于购买玉米种子,乙农户购买了4500克该玉米种子,分别计算他们的购买量和付款金额.
 某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折.某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出函数图象.如表是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10).请你结合表格和图象:
某玉米种子的价格为a元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折.某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出函数图象.如表是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为(2,10).请你结合表格和图象:| 付款金额(元) | a | 7.5 | 10 | 12 | b |
| 购买量(千克) | 1 | 1.5 | 2 | 2.5 | 3 |
(2)求出当x>2时,y关于x的函数解析式;
(3)甲农户将8.8元钱全部用于购买玉米种子,乙农户购买了4500克该玉米种子,分别计算他们的购买量和付款金额.