题目内容
12.在△ABC中,∠A=2∠B=3∠C,则△ABC按角分的形状是钝角 三角形.分析 先根据三角形内角和定理,求得∠A的度数,再根据∠A的度数,判断三角形ABC的形状.
解答 解:∵∠A=2∠B=3∠C,且∠A+∠B+∠C=180°,
∴∠A+$\frac{1}{2}$∠A+$\frac{1}{3}$∠A=180°,
解得∠A=$\frac{1080°}{11}$>90°,
∴△ABC是钝角三角形.
故答案为:钝角
点评 本题主要考查了三角形内角和定理,解决问题的关键是掌握:三角形内角和是180°.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
7.抛物线y=x2+2x-1与坐标轴的交点个数有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
7.观察下列等式:a1=n,a2=1-$\frac{1}{{a}_{{1}_{\;}}}$,a3=1-$\frac{1}{{a}_{2}}$,a4=1-$\frac{1}{{a}_{3}}$,…根据其蕴含的规律可得( )
| A. | a2016=n | B. | a2016=$\frac{n-1}{n}$ | C. | a2016=$\frac{1}{n-1}$ | D. | a2016=$\frac{1}{1-n}$ |
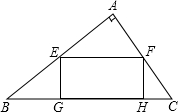 如图,△ABC是一块直角三角形材料,∠BAC=90°,BC=100cm,AB=80cm,要把它加工成矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.
如图,△ABC是一块直角三角形材料,∠BAC=90°,BC=100cm,AB=80cm,要把它加工成矩形零件,使矩形一边在BC上,其余两个顶点分别在AB、AC上.