题目内容
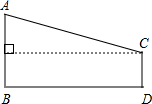 如图,磐石某风景名胜为了方便游人参观,从主峰A处假设了一条揽车线路到另一山峰C处,若主峰A的高度AB=120米,山峰C的高度CD=20米,两山峰的底部BD相距900米,求缆车线路AC的长.
如图,磐石某风景名胜为了方便游人参观,从主峰A处假设了一条揽车线路到另一山峰C处,若主峰A的高度AB=120米,山峰C的高度CD=20米,两山峰的底部BD相距900米,求缆车线路AC的长.考点:勾股定理的应用
专题:
分析:过点C作CO⊥AB,垂足为O,由图可看出,三角形OAC为一直角三角形,已知一直角边和一角,则可求斜边.
解答: 解:由题意得:AB=120米,CD=20米,
解:由题意得:AB=120米,CD=20米,
过点C作CO⊥AB,垂足为O,
∴OB=CD=20,
∴AO=AB-OB=120-20=100米,
∵两山峰的底部BD相距900米,
∴由勾股定理得:AC=
≈906m,
答:缆车线路AC的长约为906米.
 解:由题意得:AB=120米,CD=20米,
解:由题意得:AB=120米,CD=20米,过点C作CO⊥AB,垂足为O,
∴OB=CD=20,
∴AO=AB-OB=120-20=100米,
∵两山峰的底部BD相距900米,
∴由勾股定理得:AC=
| 9002+1002 |
答:缆车线路AC的长约为906米.
点评:本题考查了直角三角形的性质和勾股定理,正确的运算是解答本题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目

 已知:如图,在△ABC中,AD是角平分线,BE⊥AD,交AD的延长线于点E,点F在AB上,且∠FBE=∠FEB,试说明:EF∥AC.
已知:如图,在△ABC中,AD是角平分线,BE⊥AD,交AD的延长线于点E,点F在AB上,且∠FBE=∠FEB,试说明:EF∥AC.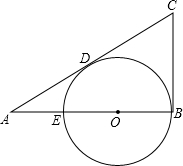 如图,△ABC中,∠B=90°,0为AB上一点,以0为圆心,以OB为半径的圆切AC于D点,交AB于E点,AD=2,AE=1,求CD.
如图,△ABC中,∠B=90°,0为AB上一点,以0为圆心,以OB为半径的圆切AC于D点,交AB于E点,AD=2,AE=1,求CD.