题目内容
已知a＜3，解关于x的不等式ax＜3x+2．
考点：解一元一次不等式
专题：
分析：首先移项，然后合并同类项，根据a的范围，把系数化为1即可求解．
解答：解：移项，得：ax-3x＜2，
合并同类项，得：（a-3）x＜2，
∵a＜3，
∴a-3＜0，
∴不等式的解集是：x＞
．
合并同类项，得：（a-3）x＜2，
∵a＜3，
∴a-3＜0，
∴不等式的解集是：x＞
| 2 |
| a-3 |
点评：本题考查了解简单不等式的能力，解答这类题学生往往在解题时不注意移项要改变符号这一点而出错．
解不等式要依据不等式的基本性质，在不等式的两边同时加上或减去同一个数或整式不等号的方向不变；在不等式的两边同时乘以或除以同一个正数不等号的方向不变；在不等式的两边同时乘以或除以同一个负数不等号的方向改变．
解不等式要依据不等式的基本性质，在不等式的两边同时加上或减去同一个数或整式不等号的方向不变；在不等式的两边同时乘以或除以同一个正数不等号的方向不变；在不等式的两边同时乘以或除以同一个负数不等号的方向改变．
练习册系列答案
相关题目
要使二次根式
有意义，字母x必须满足的条件是（ ）
| x2+1 |
| A、x≥1 | B、x＞0 |
| C、x≥-1 | D、任意实数 |
如图，线段AB、DC分别表示甲、乙两建筑物的高，AB⊥BC于B，DC⊥BC于C，从B点测得D点的仰角α为60°从A点测得D点的仰角β为15°，已知甲建筑物AB的高为36米．
如图，在我国沿海有一艘不明国籍的轮船进入我国海域，我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截，六分钟后同时到达C地将其拦截．已知甲巡逻艇每小时航行120海里，乙巡逻艇每小时航行50海里，航向为北偏西40°，问：甲巡逻艇的航向？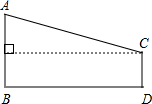
如图，磐石某风景名胜为了方便游人参观，从主峰A处假设了一条揽车线路到另一山峰C处，若主峰A的高度AB=120米，山峰C的高度CD=20米，两山峰的底部BD相距900米，求缆车线路AC的长．
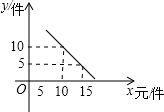某文具零售店准备从批发市场选购A、B两种文具，批发价A种为12元/件，B种为8元/件．若该店零售A、B两种文具的日销量y（件）与零售价x（元/件）均成如图的一次函数关系．