题目内容
已知直线y=kx+b与直线y=-3x平行且过点(3,3).
(1)求k,b的值;
(2)若直线y=kx+b分别与x,y轴交于点A,B.若点P(x,y)在直线AB上,且△POB为等腰三角形.求出所有符合条件的P的坐标.
(1)求k,b的值;
(2)若直线y=kx+b分别与x,y轴交于点A,B.若点P(x,y)在直线AB上,且△POB为等腰三角形.求出所有符合条件的P的坐标.
考点:两条直线相交或平行问题
专题:
分析:(1)根据直线y=kx+b与直线y=-3x平行且过点(3,3),直接代入求出k、b的值;
(2)先求出点A,B的坐标和OB、OA、AB的长,再分当BP1=B0时,当BP2=0P2时,当BP3=B0时,当OP4=B0时,△POB为等腰三角形四种情况讨论,分别进行计算即可求出P的坐标.
(2)先求出点A,B的坐标和OB、OA、AB的长,再分当BP1=B0时,当BP2=0P2时,当BP3=B0时,当OP4=B0时,△POB为等腰三角形四种情况讨论,分别进行计算即可求出P的坐标.
解答: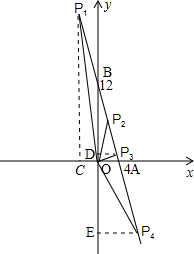 解:(1)∵直线y=kx+b与直线y=-3x平行且过点(3,3),
解:(1)∵直线y=kx+b与直线y=-3x平行且过点(3,3),
∴k=-3,3=3k+b,
∴b=12;
(2)∵直线y=-3x+12分别与x,y轴交于点A,B,
∴点A,B的坐标分别为:(4,0),(0,12),
∴OB=12,OA=4,
∴AB=4
,
如图;
当BP1=B0时,△POB为等腰三角形,过P1作P1C⊥x轴,
则
=
,
=
,
=
,
=
,
CP1=12+
,CO=
,
此时点P的坐标是(-
,12+
);
当BP2=0P2时,△POB为等腰三角形,
则点P2在OP的垂直平分线上,则点P2的纵坐标是6,横坐标是2,
此时点P的坐标是(2,6);
当BP3=B0时,△POB为等腰三角形,过P3作P3D⊥y轴,
则
=
=
,
=
=
,
BD=
,P3D=
,
则OD=12-
,
此时点P的坐标是(
,12-
);
当OP4=B0时,△POB为等腰三角形,过P4作P4E⊥y轴,设P4点的横坐标为m,则P4E=m,BE=3m,
则m2+(3m-12)2=122,
解得:m=0(舍去)或m=9,
此时点P的坐标是(9,-15);
综上所述,点P的坐标是(-
,12+
)、(2,6)、(
,12-
)、(9,-15).
 解:(1)∵直线y=kx+b与直线y=-3x平行且过点(3,3),
解:(1)∵直线y=kx+b与直线y=-3x平行且过点(3,3),∴k=-3,3=3k+b,
∴b=12;
(2)∵直线y=-3x+12分别与x,y轴交于点A,B,
∴点A,B的坐标分别为:(4,0),(0,12),
∴OB=12,OA=4,
∴AB=4
| 10 |
如图;
当BP1=B0时,△POB为等腰三角形,过P1作P1C⊥x轴,
则
| AB |
| AP1 |
| BO |
| CP1 |
| AB |
| BP1 |
| AO |
| CO |
4
| ||
4
|
| 12 |
| CP1 |
4
| ||
| 12 |
| 4 |
| CO |
CP1=12+
| 18 |
| 5 |
| 10 |
6
| ||
| 5 |
此时点P的坐标是(-
6
| ||
| 5 |
| 18 |
| 5 |
| 10 |
当BP2=0P2时,△POB为等腰三角形,
则点P2在OP的垂直平分线上,则点P2的纵坐标是6,横坐标是2,
此时点P的坐标是(2,6);
当BP3=B0时,△POB为等腰三角形,过P3作P3D⊥y轴,
则
| BD |
| BO |
| BP3 |
| BA |
| P3D |
| AO |
| BD |
| 12 |
| 12 | ||
4
|
| P3D |
| 4 |
BD=
18
| ||
| 5 |
9
| ||
| 10 |
则OD=12-
18
| ||
| 5 |
此时点P的坐标是(
9
| ||
| 10 |
18
| ||
| 5 |
当OP4=B0时,△POB为等腰三角形,过P4作P4E⊥y轴,设P4点的横坐标为m,则P4E=m,BE=3m,
则m2+(3m-12)2=122,
解得:m=0(舍去)或m=9,
此时点P的坐标是(9,-15);
综上所述,点P的坐标是(-
6
| ||
| 5 |
| 18 |
| 5 |
| 10 |
9
| ||
| 10 |
18
| ||
| 5 |
点评:此题考查了两直线平行问题;用到的知识点为:两直线平行、比例系数相等、勾股定理、平行线分线段成比例定理,注意把点P的所有坐标都求出.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
直角三角形一直角边长为4,另一边长为5,则其周长为( )
| A、12 | ||
B、12或9+
| ||
C、9+
| ||
| D、以上答案都不对 |
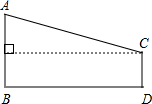 如图,磐石某风景名胜为了方便游人参观,从主峰A处假设了一条揽车线路到另一山峰C处,若主峰A的高度AB=120米,山峰C的高度CD=20米,两山峰的底部BD相距900米,求缆车线路AC的长.
如图,磐石某风景名胜为了方便游人参观,从主峰A处假设了一条揽车线路到另一山峰C处,若主峰A的高度AB=120米,山峰C的高度CD=20米,两山峰的底部BD相距900米,求缆车线路AC的长.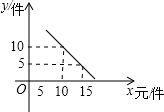 某文具零售店准备从批发市场选购A、B两种文具,批发价A种为12元/件,B种为8元/件.若该店零售A、B两种文具的日销量y(件)与零售价x(元/件)均成如图的一次函数关系.
某文具零售店准备从批发市场选购A、B两种文具,批发价A种为12元/件,B种为8元/件.若该店零售A、B两种文具的日销量y(件)与零售价x(元/件)均成如图的一次函数关系.
 如图,△ABC中,AB=5,cosB=
如图,△ABC中,AB=5,cosB=