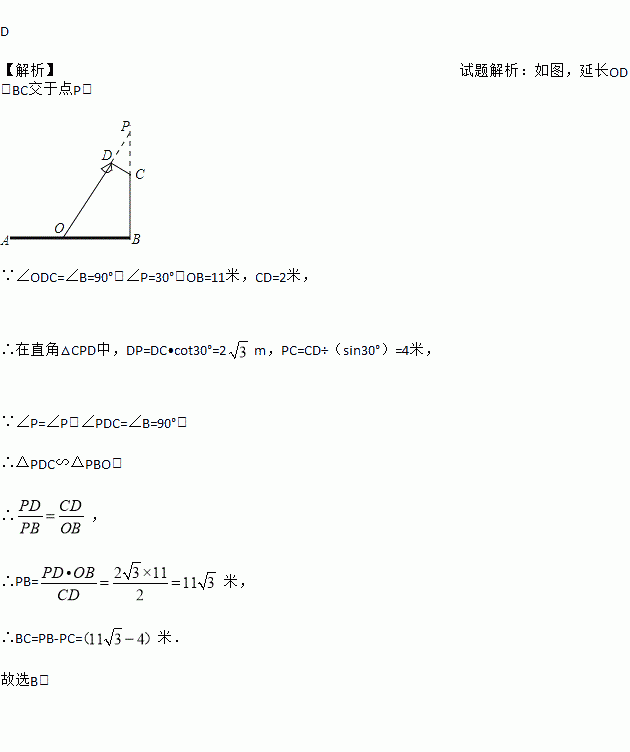题目内容
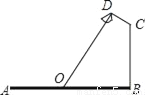
如图，要在宽为22米的九州大道两边安装路灯，路灯的灯臂CD长2米，且与灯柱BC成120°角，路灯采用圆锥形灯罩，灯罩的轴线DO与灯臂CD垂直，当灯罩的轴线DO通过公路路面的中心线时照明效果最佳，此时，路灯的灯柱BC高度应该设计为（ ）
A. （11﹣2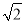
）米 B. （11
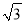﹣2
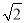）米 C. （11﹣2
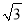）米 D. （11
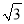﹣4）米
D
【解析】试题解析：如图，延长OD，BC交于点P．
∵∠ODC=∠B=90°，∠P=30°，OB=11米，CD=2米，
∴在直角△CPD中，DP=DC•cot30°=2m，PC=CD÷（sin30°）=4米，
∵∠P=∠P，∠PDC=∠B=90°，
∴△PDC∽△PBO，
∴，
∴PB=米，
∴BC=PB-PC=米．
故选B．
口算题卡北京妇女儿童出版社系列答案如图所示，已知抛物线P：y＝ax2＋bx＋c(a≠0)与x轴交于A，B两点(点A在x轴的正半轴上)，与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F，G分别在线段BC，AC上，抛物线P上的部分点的横坐标对应的纵坐标如下.
(1)求A，B，C三点的坐标；
(2)若点D的坐标为(m，0)，矩形DEFG的面积为S，求S与m的函数关系式，并指出m的取值范围；
(3)当矩形DEFG的面积S最大时，连接DF并延长至点M，使FM＝k·DF，若点M不在抛物线P上，求k的取值范围；
(4)若点D的坐标为(1，0)，求矩形DEFG的面积．
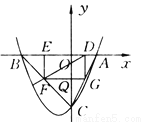
（1）A(2，0)，B(－4，0)，C(0，－4)；（2）S矩形DEFG=12m－6m2(0＜m＜2)；（3）k的取值范围是k≠且k＞0；（4）S矩形DEFG＝6．
【解析】试题分析：（1）可任选三组坐标，用待定系数法即可求出抛物线P的解析式．然后根据抛物线P的解析式即可得出A、B、C三点的坐标；
（2）求矩形的面积需知道矩形的长和宽，可先在直角三角形AOC中，根据AD，OA，DG，C... 已知抛物线y＝x2－2x＋m＋1与x轴有两个不同的交点，则函数y＝
的大致图象是( )
A. （A） B. （B） C. （C） D. （D）
A
【解析】抛物线y=x2-2x+m+1与x轴有两个不同的交点，可得△=（-2）2-4（m+1）＞0，解得m＜0，因此可得函数y=的图象位于二、四象限，
故选：A． 拦水坝横断面如图所示,迎水坡AB的坡比是1∶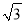
,坝高BC=10 m,则坡面AB的长度是( )
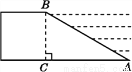
A. 15 m B. 20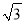
m C. 10
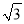m D. 20 m
D
【解析】在Rt△ABC中，BC＝10m， ，∴ (m)，
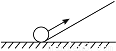
∴．故选D． 如图，一个小球由地面沿着坡度i=1∶2的坡面向上前进了10 m，此时小球距离地面的高度为( )．
A．5m B．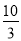
m C．4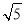
m D．2
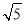m
D.
【解析】
试题分析：画出草图，根据题意用未知数表示相应的线段的长度，再运用勾股定理列方程求解即可．
试题解析：如图：
Rt△ABC中，tanA=，AB=10．
设BC=x，则AC=2x，
∴x2+（2x）2=102，
解得，（负值舍去）．
即此时小球距离地面的高度为米．
故选D. 如果水流的速度为a m/min(定量)，那么每分钟的进水量Q(m3)与所选择的水管直径D(m)之间的函数关系式是什么?
Q＝.
【解析】试题分析：根据圆柱体的体积公式V=πr2h，直接代入求解即可.
试题解析：函数关系式为Q＝a·π·()2＝ . 图中的圆点是有规律地从里到外逐层排列的．设y为第n层（n为正整数）圆点的个数，则下列函数关系中正确的是（ ）
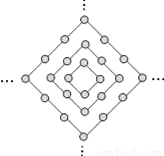
A. y=4n﹣4 B. y=4n C. y=4n+4 D. y=n2
B
【解析】试题解析：由题图可知：
n=1时，圆点有4个，即y=4；
n=2时，圆点有8个，即y=8；
n=3时，圆点有12个，即y=12；
……
∴y=4n.
故选：B. 观察下列各式：①2a＋b和a＋b，②5m（a－b）和－a＋b，③3（a＋b）和－a－b，④x2－y2和x2+y2。其中有公因式的是（ ）
A．①② B.②③ C．③④ D．①④
B
【解析】
试题分析：根据公因式的定义依次分析各小题即可判断.
①2a＋b和a＋b，④x2－y2和x2+y2，没有公因式；
②5m（a－b）和－a＋b=－（a－b），公因式为a－b，③3（a＋b）和－a－b=－（a＋b），公因式为a+b，
故选B. 若点A（2， 
），B（-3，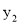 
），C（-1， 
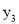）三点在抛物线
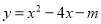的图象上，则
、
、
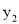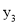的大小关系是（ ）
A.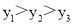 
B.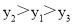 
C.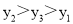 
D.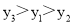 
C
【解析】首先求出二次函数的图象的对称轴x==2，且由a=1＞0，可知其开口向上，然后由A（2， ）中x=2，知最小，再由B（-3， ），C（-1， ）都在对称轴的左侧，而在对称轴的左侧，y随x得增大而减小，所以．总结可得．
故选：C．