题目内容
如果水流的速度为a m/min(定量)，那么每分钟的进水量Q(m3)与所选择的水管直径D(m)之间的函数关系式是什么?
Q＝.
【解析】试题分析：根据圆柱体的体积公式V=πr2h，直接代入求解即可.
试题解析：函数关系式为Q＝a·π·()2＝ .
练习册系列答案
相关题目
在体育测试时，初三的一名高个子男生推铅球，已知铅球所经过的路线是某二次函数图象的一部分(如图)，若这个男生出手处A点的坐标为(0，2)，铅球路线的最高处B点的坐标为B(6，5).
(1)求这个二次函数的表达式；
(2)该男生把铅球推出去多远?(精确到0.01米).
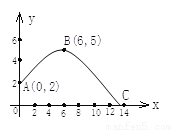
（1）y= (x-6)2+5；（2）该男生把铅球推出约13.75米
【解析】试题分析：（1）根据顶点坐标B(6,5)可设函数关系式为y=a(x-6)2+5，再把A(0,2)代入即可求得结果；
（2）把y=0代入求得图象与x轴的交点坐标，即可得到结果.
(1)设y=a(x-6)2+5,
则由A(0,2)得2=a(0-6)2+5，解得a=.
故y= (x-6)2+5；
... 小明乘滑草车沿坡比为1：2.4的斜坡下滑130米，求他下降的高度
50米
【解析】试题分析：根据坡比可设BC=x，AC=2.4x，根据勾股定理得出AB=2.6x，根据AB的长度得出x的值，从而得出BC的值，即下降的高度．
试题解析：∵坡比为1：2.4， ∴BC：AC=1：2.4， 设BC=x，AC=2.4x，
则AB= ∵AB=130米， ∴x=50， 则BC=x=50（米）． 一斜坡长为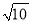
米，高度为1米，那么坡比为（ ）
A. 1：3 B. 1：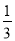 
C. 1： 
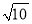D. 1：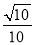 
A
【解析】试题分析：根据斜坡的长度和高度可以得出斜坡的水平距离为3米，则坡比=垂直高度：水平距离=1：3，故选A． 如图，要在宽为22米的九州大道两边安装路灯，路灯的灯臂CD长2米，且与灯柱BC成120°角，路灯采用圆锥形灯罩，灯罩的轴线DO与灯臂CD垂直，当灯罩的轴线DO通过公路路面的中心线时照明效果最佳，此时，路灯的灯柱BC高度应该设计为（ ）
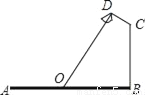
A. （11﹣2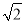
）米 B. （11
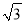﹣2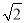
）米 C. （11﹣2
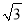）米 D. （11
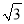﹣4）米
D
【解析】试题解析：如图，延长OD，BC交于点P．
∵∠ODC=∠B=90°，∠P=30°，OB=11米，CD=2米，
∴在直角△CPD中，DP=DC•cot30°=2m，PC=CD÷（sin30°）=4米，
∵∠P=∠P，∠PDC=∠B=90°，
∴△PDC∽△PBO，
∴，
∴PB=米，
∴BC=PB-PC=米．
故选B． 若y＝(m2－3m)x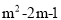
是二次函数，则m＝____．
-1
【解析】由二次函数的定义可知自变量的最高指数为2，且系数不等于0，可得m2－3m≠0，且；解得m=-1或m=3；当m=3时，m2－3m=0；最终可求得m=-1．
故答案为：-1. 下列函数中属于一次函数的是( )，属于反比例函数的是( )，属于二次函数的是( )
A. y＝x(x＋1) B. xy＝1
C. y＝2x2－2(x＋1)2 D.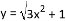 
CBA
【解析】根据题意可知y=x（x+1）=x2+x，可由二次函数的定义，可知是二次函数；根据xy=1是反比例关系，所以是反比例函数；而y＝2x2－2(x＋1)2= y＝2x2－2(x2+2x+1)=-4x-2，是一次函数；函数是带二次根号的函数.
故答案为：C、B、A. 下列各式公因式是a的是（ ）
A. ax＋ay＋5 B．3ma－6ma2 C．4a2＋10ab D．a2－2a＋ma
D
【解析】
试题分析：根据公因式的定义依次分析各项即可判断.
A．ax＋ay＋5没有公因式，B．3ma－6ma2公因式是3ma，C．4a2＋10ab公因式是2a，故错误；
D．a2－2a＋ma公因式是a，本选项正确. 如图图形中，阴影部分面积相等的是（ ）
A. 甲 乙
B. 甲 丙
C. 乙 丙
D. 丙 丁
B
【解析】根据题意，可知：
甲：直线与x轴交点为（3，0），与y轴的交点为（0，4），则阴影部分的面积为×3×4=6；
乙：阴影部分为斜边为4的等腰直角三角形，其面积为×4×2=4；
丙：抛物线与x轴的两个交点为（-3，0）与（3，0），顶点坐标为（0，-2），则阴影部分的面积为×6×2=6；
丁：此函数是反比例函数，那么阴影部分的面积为×6=3；
因此甲、丙...