题目内容
图中的圆点是有规律地从里到外逐层排列的．设y为第n层（n为正整数）圆点的个数，则下列函数关系中正确的是（ ）
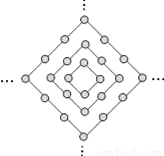
A. y=4n﹣4 B. y=4n C. y=4n+4 D. y=n2
B
【解析】试题解析：由题图可知：
n=1时，圆点有4个，即y=4；
n=2时，圆点有8个，即y=8；
n=3时，圆点有12个，即y=12；
……
∴y=4n.
故选：B.
练习册系列答案
活力课时同步练习册系列答案
学业测评一课一测系列答案
相关题目
不论m为何实数，抛物线y＝x2－mx＋m－2（ ）
A.在x轴上方 B.与x轴只有一个交点
C.与x轴有两个交点 D.在x轴下方
C
【解析】
试题分析：，当△=-4ac>0时，函数与x轴有两个交点；当△=-4ac=0时，函数与x轴有一个交点；当△=-4ac<0时，函数与x轴没有交点.根据题意可得：△=-4(m-2)=+4>0，则函数与x轴有两个交点. 河堤横断面如图所示，堤高BC=6米，迎水坡AB的坡比为1：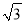 
则AB的长为_______
12米
【解析】试题分析：根据BC=6m，坡比为1： 可得：AC=6m，最后根据Rt△ABC的勾股定理可得：AB=12米． 如图，要在宽为22米的九州大道两边安装路灯，路灯的灯臂CD长2米，且与灯柱BC成120°角，路灯采用圆锥形灯罩，灯罩的轴线DO与灯臂CD垂直，当灯罩的轴线DO通过公路路面的中心线时照明效果最佳，此时，路灯的灯柱BC高度应该设计为（ ）
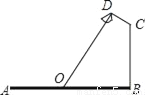
A. （11﹣2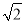
）米 B. （11
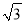﹣2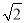
）米 C. （11﹣2
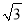）米 D. （11
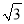﹣4）米
D
【解析】试题解析：如图，延长OD，BC交于点P．
∵∠ODC=∠B=90°，∠P=30°，OB=11米，CD=2米，
∴在直角△CPD中，DP=DC•cot30°=2m，PC=CD÷（sin30°）=4米，
∵∠P=∠P，∠PDC=∠B=90°，
∴△PDC∽△PBO，
∴，
∴PB=米，
∴BC=PB-PC=米．
故选B． 抛物线y=x2－2x+3的顶点坐标是_______．
(1，2)
【解析】试题解析：∵y=x2-2x+3=x2-2x+1-1+3=（x-1）2+2，
∴抛物线y=x2-2x+3的顶点坐标是（1，2） 下列函数中属于一次函数的是( )，属于反比例函数的是( )，属于二次函数的是( )
A. y＝x(x＋1) B. xy＝1
C. y＝2x2－2(x＋1)2 D.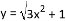 
CBA
【解析】根据题意可知y=x（x+1）=x2+x，可由二次函数的定义，可知是二次函数；根据xy=1是反比例关系，所以是反比例函数；而y＝2x2－2(x＋1)2= y＝2x2－2(x2+2x+1)=-4x-2，是一次函数；函数是带二次根号的函数.
故答案为：C、B、A. 如果x+y=5,xy=2,求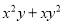
和
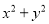的值
10；21.
【解析】试题分析：（1）因式分解后直接代入求值即可；（2）化为（x+y）2-2xy后代入求值即可.
试题解析：
∵x+y=5，xy=2，
∴=xy（x+y）=2×5=10；
=（x+y）2-2xy=52-2×2=25-4=21. 若关于x的多项式3x2+mx+n分解因式的结果为(3x+2)(x-1)，求m、n的值.
m=-1,n=-2.
【解析】试题分析：把(3x+2)(x-1)利用多项式乘以多项式的法则展开，与多项式3x2+mx+n比较，即可得m、n的值.
试题解析：
由题意可得：(3x+2)(x-1)=3x2+2x-3x-2=3x2-x-2=3x2+mx+n，
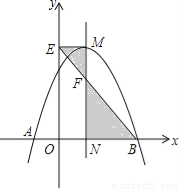
所以m=-1,n=-2. 如图，抛物线
与x轴交于A，B两点，它们的对称轴与x轴交于点N，过顶点M作ME⊥y轴于点E，连结BE交MN于点F.已知点A的坐标为（﹣1，0）.
（1）求该抛物线的解析式及顶点M的坐标；
（2）求△EMF与△BNF的面积之比.
（1），（1，4）；（2）.
【解析】试题分析：（1）直接将（﹣1，0）代入求出即可，再利用配方法求出顶点坐标.
（2）利用EM∥BN，则△EMF∽△BNF，进而求出△EMF与△BNE的面积之比．
试题解析：【解析】
（1）∵点A在抛物线上，
∴，解得：c=3，
∴抛物线的解析式为.
∵，
∴抛物线的顶点M（1，4）；
（2）∵A（﹣1，0），抛物...