题目内容
观察下列各式：①2a＋b和a＋b，②5m（a－b）和－a＋b，③3（a＋b）和－a－b，④x2－y2和x2+y2。其中有公因式的是（ ）
A．①② B.②③ C．③④ D．①④
B
【解析】
试题分析：根据公因式的定义依次分析各小题即可判断.
①2a＋b和a＋b，④x2－y2和x2+y2，没有公因式；
②5m（a－b）和－a＋b=－（a－b），公因式为a－b，③3（a＋b）和－a－b=－（a＋b），公因式为a+b，
故选B.
练习册系列答案
相关题目
开口向下的抛物线y＝(m2－2)x2＋2mx＋1的对称轴经过点(－1，3)，则m＝_____．
－1
【解析】由于抛物线y=（m2-2）x2+2mx+1的对称轴经过点（-1，3），
∴对称轴为直线x=-1，x==-1，
解得m1=-1，m2=2．
由于抛物线的开口向下，所以当m=2时，m2-2=2＞0，不合题意，应舍去，
∴m=-1．
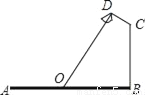
故答案为：-1. 如图，要在宽为22米的九州大道两边安装路灯，路灯的灯臂CD长2米，且与灯柱BC成120°角，路灯采用圆锥形灯罩，灯罩的轴线DO与灯臂CD垂直，当灯罩的轴线DO通过公路路面的中心线时照明效果最佳，此时，路灯的灯柱BC高度应该设计为（ ）
A. （11﹣2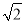
）米 B. （11
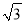﹣2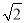
）米 C. （11﹣2
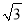）米 D. （11
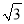﹣4）米
D
【解析】试题解析：如图，延长OD，BC交于点P．
∵∠ODC=∠B=90°，∠P=30°，OB=11米，CD=2米，
∴在直角△CPD中，DP=DC•cot30°=2m，PC=CD÷（sin30°）=4米，
∵∠P=∠P，∠PDC=∠B=90°，
∴△PDC∽△PBO，
∴，
∴PB=米，
∴BC=PB-PC=米．
故选B． 下列函数中属于一次函数的是( )，属于反比例函数的是( )，属于二次函数的是( )
A. y＝x(x＋1) B. xy＝1
C. y＝2x2－2(x＋1)2 D.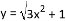 
CBA
【解析】根据题意可知y=x（x+1）=x2+x，可由二次函数的定义，可知是二次函数；根据xy=1是反比例关系，所以是反比例函数；而y＝2x2－2(x＋1)2= y＝2x2－2(x2+2x+1)=-4x-2，是一次函数；函数是带二次根号的函数.
故答案为：C、B、A. 如果x+y=5,xy=2,求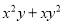
和
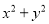的值
10；21.
【解析】试题分析：（1）因式分解后直接代入求值即可；（2）化为（x+y）2-2xy后代入求值即可.
试题解析：
∵x+y=5，xy=2，
∴=xy（x+y）=2×5=10；
=（x+y）2-2xy=52-2×2=25-4=21. 下列各式公因式是a的是（ ）
A. ax＋ay＋5 B．3ma－6ma2 C．4a2＋10ab D．a2－2a＋ma
D
【解析】
试题分析：根据公因式的定义依次分析各项即可判断.
A．ax＋ay＋5没有公因式，B．3ma－6ma2公因式是3ma，C．4a2＋10ab公因式是2a，故错误；
D．a2－2a＋ma公因式是a，本选项正确. 若关于x的多项式3x2+mx+n分解因式的结果为(3x+2)(x-1)，求m、n的值.
m=-1,n=-2.
【解析】试题分析：把(3x+2)(x-1)利用多项式乘以多项式的法则展开，与多项式3x2+mx+n比较，即可得m、n的值.
试题解析：
由题意可得：(3x+2)(x-1)=3x2+2x-3x-2=3x2-x-2=3x2+mx+n，
所以m=-1,n=-2. 已知m，n是关于x的方程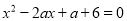
的两实根，求
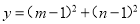的最小值．
8
【解析】试题分析：根据方程有两个根，利用根的判别式求出a的取值范围，再根据根与系数的关系求出m+n与mn的值，然后把整理成m+n与mn的形式，代入进行计算求解．
试题解析：依题意△=≥0，
即，
∴a≤-2或a≥3，
由m+n=2a，mn=a+6，
即
=
=
=，
∴a=3时，y的最小值为8．
故答案为：8． 用一根长为80cm的铁丝，把它弯成一个矩形，设矩形的面积为ycm2，一边长为xcm，则y与x的函数表达式为___________（化为一般式）
【解析】由题意得：矩形的另一边长=80÷2-x=40-x，
∴y=x（40-x）=．
故答案为：．