题目内容
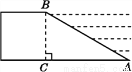
拦水坝横断面如图所示,迎水坡AB的坡比是1∶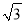
,坝高BC=10 m,则坡面AB的长度是( )
A. 15 m B. 20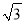
m C. 10
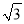m D. 20 m
D
【解析】在Rt△ABC中，BC＝10m， ，∴ (m)，
∴．故选D．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，隧道的截面是抛物线，可以用y=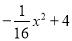 
表示，该隧道内设双行道，限高为3m，那么每条行道宽是（ ）
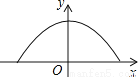
A. 不大于4m B. 恰好4m C. 不小于4m D. 大于4m，小于8m
A
【解析】把y=3代入y= 中得：
x=4，x= -4（舍去）．
∴每条行道宽应不大于4m．
故选A．
点睛；本题考查二次函数的实际应用．此题为数学建模题，借助二次函数解决实际问题．由题意可知，直接把y=3代入解析式求解即可． 开口向下的抛物线y＝(m2－2)x2＋2mx＋1的对称轴经过点(－1，3)，则m＝_____．
－1
【解析】由于抛物线y=（m2-2）x2+2mx+1的对称轴经过点（-1，3），
∴对称轴为直线x=-1，x==-1，
解得m1=-1，m2=2．
由于抛物线的开口向下，所以当m=2时，m2-2=2＞0，不合题意，应舍去，
∴m=-1．
故答案为：-1. 小明乘滑草车沿坡比为1：2.4的斜坡下滑130米，求他下降的高度
50米
【解析】试题分析：根据坡比可设BC=x，AC=2.4x，根据勾股定理得出AB=2.6x，根据AB的长度得出x的值，从而得出BC的值，即下降的高度．
试题解析：∵坡比为1：2.4， ∴BC：AC=1：2.4， 设BC=x，AC=2.4x，
则AB= ∵AB=130米， ∴x=50， 则BC=x=50（米）． 河堤横断面如图所示，堤高BC=6米，迎水坡AB的坡比为1：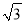 
则AB的长为_______
12米
【解析】试题分析：根据BC=6m，坡比为1： 可得：AC=6m，最后根据Rt△ABC的勾股定理可得：AB=12米． 一斜坡长为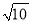
米，高度为1米，那么坡比为（ ）
A. 1：3 B. 1：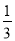 
C. 1： 
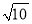D. 1：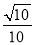 
A
【解析】试题分析：根据斜坡的长度和高度可以得出斜坡的水平距离为3米，则坡比=垂直高度：水平距离=1：3，故选A． 如图，要在宽为22米的九州大道两边安装路灯，路灯的灯臂CD长2米，且与灯柱BC成120°角，路灯采用圆锥形灯罩，灯罩的轴线DO与灯臂CD垂直，当灯罩的轴线DO通过公路路面的中心线时照明效果最佳，此时，路灯的灯柱BC高度应该设计为（ ）
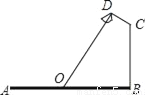
A. （11﹣2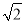
）米 B. （11
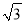﹣2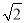
）米 C. （11﹣2
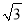）米 D. （11
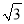﹣4）米
D
【解析】试题解析：如图，延长OD，BC交于点P．
∵∠ODC=∠B=90°，∠P=30°，OB=11米，CD=2米，
∴在直角△CPD中，DP=DC•cot30°=2m，PC=CD÷（sin30°）=4米，
∵∠P=∠P，∠PDC=∠B=90°，
∴△PDC∽△PBO，
∴，
∴PB=米，
∴BC=PB-PC=米．
故选B． 下列函数中属于一次函数的是( )，属于反比例函数的是( )，属于二次函数的是( )
A. y＝x(x＋1) B. xy＝1
C. y＝2x2－2(x＋1)2 D.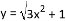 
CBA
【解析】根据题意可知y=x（x+1）=x2+x，可由二次函数的定义，可知是二次函数；根据xy=1是反比例关系，所以是反比例函数；而y＝2x2－2(x＋1)2= y＝2x2－2(x2+2x+1)=-4x-2，是一次函数；函数是带二次根号的函数.
故答案为：C、B、A. 已知m，n是关于x的方程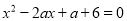
的两实根，求
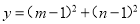的最小值．
8
【解析】试题分析：根据方程有两个根，利用根的判别式求出a的取值范围，再根据根与系数的关系求出m+n与mn的值，然后把整理成m+n与mn的形式，代入进行计算求解．
试题解析：依题意△=≥0，
即，
∴a≤-2或a≥3，
由m+n=2a，mn=a+6，
即
=
=
=，
∴a=3时，y的最小值为8．
故答案为：8．