题目内容
6．在实数$\sqrt{2}$+1、-3、$\sqrt{99}$、0、$\root{3}{-1}$、3.1415、π、$\sqrt{144}$、0.6060060006…（两个6之间依次多一个0）中无理数有4个．分析 无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
解答 解：$\sqrt{2}$+1、$\sqrt{99}$、π、0.6060060006…（两个6之间依次多一个0）是无理数，
故答案为：4．
点评 此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，$\sqrt{6}$，0.8080080008…（每两个8之间依次多1个0）等形式．
练习册系列答案
相关题目
16．
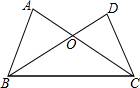如图，下列条件中，不能证明△ABC≌△DCB的是（ ）
如图，下列条件中，不能证明△ABC≌△DCB的是（ ）| A． | AB=DC，AC=DB | B． | AB=DC，∠ABC=∠DCB | C． | AC=BD，∠A=∠D | D． | BO=CO，∠A=∠D |
如图所示，等边三角形ABC的边长为3，P为BC上一点，且BP=1，D为AC上一点，若∠APD=60°，求CD的长．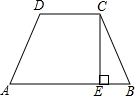
已知在梯形ABCD中，AB∥CD，CE⊥AB，垂足为E，梯形的面积为80，CE=8．
如图，已知AD⊥BC于点O，且O是BC的中点，增加一个条件后可利用“HL”证明△AOB≌△DOC，则所增加的条件是AB=CD．