题目内容
18. 如图,已知AD⊥BC于点O,且O是BC的中点,增加一个条件后可利用“HL”证明△AOB≌△DOC,则所增加的条件是AB=CD.
如图,已知AD⊥BC于点O,且O是BC的中点,增加一个条件后可利用“HL”证明△AOB≌△DOC,则所增加的条件是AB=CD.
分析 根据斜边和一条直角边对应相等的两个直角三角形全等进行判断即可.
解答 解:增加的条件是:AB=CD.
∵O是BC的中点,
∴BO=CO,
∵AD⊥BC,
∴△AOB和△COD是直角三角形,
在Rt△AOB和Rt△DOC中,
$\left\{\begin{array}{l}{AB=CD}\\{BO=CO}\end{array}\right.$,
∴Rt△AOB≌Rt△DOC(HL),
故答案为:AB=CD.
点评 本题主要考查了全等三角形的判定,解题时注意:斜边和一条直角边对应相等的两个直角三角形全等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.已知,x,y,z为三个非负实数,且满足$\left\{\begin{array}{l}{3x+2y+z=5}\\{2x+y-3z=1}\end{array}\right.$,设S=3x+y-7z,则S的最大值是( )
| A. | -$\frac{1}{11}$ | B. | $\frac{1}{11}$ | C. | -$\frac{5}{7}$ | D. | -$\frac{7}{5}$ |
10.实数$\root{3}{27}$,0,-π,$\sqrt{16}$,$\sqrt{8}$,$\frac{1}{3}$,0.101 001 0001…(相邻两个1之间多一个0),其中无理数有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
8.直角三角形两直角边分别为5cm和12cm,则其斜边的高为( )
| A. | 6cm | B. | 8cm | C. | $\frac{80}{13}$cm | D. | $\frac{60}{13}$cm |
 如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BE⊥AD交AC的延长线于点F,E为垂足,则结论::①AD=BF;②CF=CD;③AC+CD=AB;④BE=CF;⑤BF=2BE,其中正确结论的个数是( )
如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BE⊥AD交AC的延长线于点F,E为垂足,则结论::①AD=BF;②CF=CD;③AC+CD=AB;④BE=CF;⑤BF=2BE,其中正确结论的个数是( )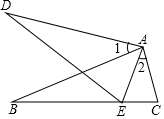 如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.
如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.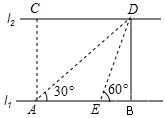 如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进60米到达点E(点E在线段AB上),测得∠DEB=60°,求河的宽度.
如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进60米到达点E(点E在线段AB上),测得∠DEB=60°,求河的宽度.