题目内容
14. 如图所示,等边三角形ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,求CD的长.
如图所示,等边三角形ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,求CD的长.
分析 由等边三角形ABC中,∠APD=60°,易得∠B=∠C=60°,∠BAP=∠DPC,则可证得△BAP∽△CPD,然后由相似三角形的对应边成比例,求得答案.
解答 解:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠APD+∠DPC=∠B+∠BAP,∠APD=60°,
∴∠BAP=∠DPC,
∴△BAP∽△CPD,
∴AB:PC=BP:CD,
∵AB=BC=3,BP=1,
∴PC=BC-BP=2,
∴3:2=1:CD,
解得:CD=$\frac{2}{3}$.
点评 此题考查了相似三角形的判定与性质以及等边三角形的性质.注意证得△BAP∽△CPD是关键.

练习册系列答案
相关题目
4.下列说法中,正确的是( )
| A. | 一个有理数不是正有理数就是负有理数 | |
| B. | 0是整数但不是正数 | |
| C. | 非正数是指负整数和负分数 | |
| D. | 一个整数不是正整数就是负整数 |
2.2015年12月15日,我国“玉兔号”月球车顺利抵达月球表面,月球离地面平均距离是384400000米,数据38400000用科学记数法表示为( )
| A. | 3.844×106 | B. | 3.844×107 | C. | 3.844×108 | D. | 3.844×109 |
4.下列说法中,不正确的是( )
| A. | 棱锥的侧面都是三角形 | B. | 棱柱的上下底面一样大 | ||
| C. | 正方体、长方体都是棱柱 | D. | 四棱锥与四棱柱的棱数一样多 |
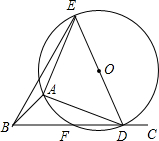 如图,∠ABC=45°,△ADE是等腰直角三角形,AE=AD,顶点A,D分别在∠ABC的两边BA,BC上滑动(不与点B重合),△ADE的外接圆交BC于点F,O为圆心.
如图,∠ABC=45°,△ADE是等腰直角三角形,AE=AD,顶点A,D分别在∠ABC的两边BA,BC上滑动(不与点B重合),△ADE的外接圆交BC于点F,O为圆心.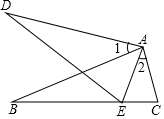 如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.
如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.