题目内容
1.若a,b都是不为零的有理数,那么$\frac{|a|}{a}$+$\frac{|b|}{b}$的值是2,0或-2.分析 分情况讨论①a>0,b>0;②a>0,b<0或a<0,b>0,③a<0,b<0,然后根据范围去掉绝对值可得出$\frac{|a|}{a}$+$\frac{|b|}{b}$可能的值.
解答 解:①a>0,b>0;
则$\frac{|a|}{a}$+$\frac{|b|}{b}$=1+1=2,
②a>0,b<0或a<0,b>0,
则$\frac{|a|}{a}$+$\frac{|b|}{b}$=1-1=0或$\frac{|a|}{a}$+$\frac{|b|}{b}$=-1+1=0
③a<0,b<0,
则$\frac{|a|}{a}$+$\frac{|b|}{b}$=-1-1=-2.
所以$\frac{|a|}{a}$+$\frac{|b|}{b}$的值是2,0或-2.
故答案为:2,0或-2.
点评 本题考查有理数的除法及绝对值的知识,难度不大,关键是分类讨论a和b的范围.

练习册系列答案
相关题目
12.下列式子去括号正确的是( )
| A. | -(2a-b)=-2a-b | B. | 3a+(4a2+2)=3a+4a2-2 | ||
| C. | -(2a+3y)=2a-3y | D. | -2(a-6)=-2a+12 |
16.下列各式结果为负数的是( )
| A. | -(-1) | B. | -|-1| | C. | (-1)4 | D. | |1-2| |
13.已知,x,y,z为三个非负实数,且满足$\left\{\begin{array}{l}{3x+2y+z=5}\\{2x+y-3z=1}\end{array}\right.$,设S=3x+y-7z,则S的最大值是( )
| A. | -$\frac{1}{11}$ | B. | $\frac{1}{11}$ | C. | -$\frac{5}{7}$ | D. | -$\frac{7}{5}$ |
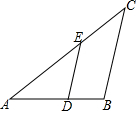 如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=6cm,∠BAC=∠C=40°.
如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=6cm,∠BAC=∠C=40°. 如图,在直角坐标系中以原点O为圆心的圆的半径由内向外依次Wie1,2,3,4,…,圆与直线y=x和y=-x分别交于:A2,A3,A4,…则点A80的坐标是(-4$\sqrt{2}$,4$\sqrt{2}$).
如图,在直角坐标系中以原点O为圆心的圆的半径由内向外依次Wie1,2,3,4,…,圆与直线y=x和y=-x分别交于:A2,A3,A4,…则点A80的坐标是(-4$\sqrt{2}$,4$\sqrt{2}$).