题目内容
17.下列说法正确的是( )| A. | △ABC的两边长AB=5,AC=12,则BC=13 | |
| B. | Rt△ABC中a=6,b=8,则c=10 | |
| C. | Rt△ABC中a=3,b=4,则△ABC的面积S=6 | |
| D. | 等边△ABC的边长为12,则高AD=6$\sqrt{3}$ |
分析 由勾股定理求出选项A、B、C不正确;由等边三角形的性质和勾股定理得出选项D正确即可.
解答 解:A、△ABC的两边长AB=5,AC=12,则BC=13,不正确;
B、Rt△ABC中a=6,b=8,则c=10,不正确;
C、Rt△ABC中a=3,b=4,则△ABC的面积S=6,不正确;
D、等边△ABC的边长为12,则高AD=6$\sqrt{3}$,正确;
故选:D.
点评 本题考查了勾股定理、等边三角形的性质、三角形面积的计算;熟练掌握勾股定理,熟记直角三角形的斜边的平方等于两条直角边长的平方和是解决问题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
8.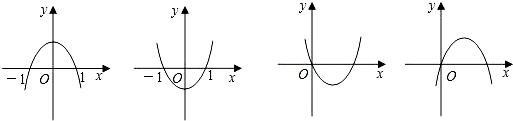 设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )
设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )
 设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )
设a、b为常数,且b>0,抛物线y=ax2+bx+a2-5a-6为下列图形之一,则a的值为( )| A. | 6或-1 | B. | -6或 1 | C. | 6 | D. | -1 |
12.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和b之间的距离是( )
| A. | 2cm | B. | 6cm | C. | 8cm | D. | 2cm或8cm |
2.对于函数y=-2x+1,下列结论正确的是( )
| A. | 它的图象必经过点(-1,2) | B. | 它的图象经过第一、二、三象限 | ||
| C. | 当x>1时,y<0 | D. | y的值随x值的增大而增大 |
9.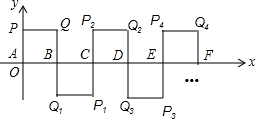 如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )
如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )
 如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )
如图所示,在平面直角坐标系中A(0,0),B(1,0),P(0,1),四边形ABQP是正方形,把正方形ABQP绕点B顺时针旋转180°,得到正方形CBQ1P1;把正方形CBQ1P1绕点C顺时针旋转180°,得到正方形CDQ2P2;依此类推,则旋转第2016次后,得到的正方形的顶点P2016的坐标为( )| A. | (2016,1) | B. | (2015,1) | C. | (2016,-1) | D. | (4032,1) |
7. 如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )
 如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )| A. | k1>k2>k3 | B. | k2>k3>k1 | C. | k3>k2>k1 | D. | k3>k1>k2 |