题目内容
7. 如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )
如图是三个反比例函数y=$\frac{{k}_{1}}{x}$,y=$\frac{{k}_{2}}{x}$,y=$\frac{{k}_{3}}{x}$在x轴上方的图象,由此观察k1,k2,k3的大小关系为( )| A. | k1>k2>k3 | B. | k2>k3>k1 | C. | k3>k2>k1 | D. | k3>k1>k2 |
分析 先根据反比例函数所在的象限判断出k1,k2,k3的符号,再在x轴上任取一点,找出y的对应值即可判断出k2,k3的大小.
解答 解:由反比例函数y=$\frac{k}{x}$的图象和性质可估算k1<0,k2>0,k3>0,
在x轴上任取一值x0且x0>0,x0为定值,
则有y1=$\frac{{k}_{0}}{{x}_{0}}$,y2=$\frac{{k}_{3}}{{x}_{0}}$且y1<y2,
∴k3>k2,
∴k3>k2>k1,
故选:C.
点评 本题考查的是反比例函数图象上点的坐标特点,解答此题的关键是熟知反比例函数的增减性及平面直角坐标系中每个象限内点的坐标特点.

练习册系列答案
相关题目
17.下列说法正确的是( )
| A. | △ABC的两边长AB=5,AC=12,则BC=13 | |
| B. | Rt△ABC中a=6,b=8,则c=10 | |
| C. | Rt△ABC中a=3,b=4,则△ABC的面积S=6 | |
| D. | 等边△ABC的边长为12,则高AD=6$\sqrt{3}$ |
15. 现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )
现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )
 现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )
现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )| A. | 0.8πcm2 | B. | 3.2πcm2 | C. | 4πcm2 | D. | 4.8πcm2 |
12.一影院观众席中的9排23号记作(9,23),那么15排42号的位置应记作( )
| A. | (42,15) | B. | (1,4) | C. | (15,42) | D. | (15,4) |
19.已知点P(a+1,2a-1)关于x轴的对称点在第一象限,则a的取值范围是( )
| A. | a>-1 | B. | a<$\frac{1}{2}$ | C. | -1$<a<\frac{1}{2}$ | D. | -1$≤a≤\frac{1}{2}$ |
17. 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )
 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )| A. | 8+6$\sqrt{3}$ | B. | 12$\sqrt{3}$ | C. | 19.2 | D. | 20 |
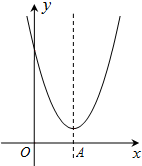 如图,二次函数y=x2-4x+3+$\sqrt{3}$的图象的对称轴交x轴于A点.
如图,二次函数y=x2-4x+3+$\sqrt{3}$的图象的对称轴交x轴于A点. 如图,若A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,若A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.