题目内容
6.已知A(-1,y1)、B(3,y2)为一次函数y=-2x+3图象上的两点,则y1与y2的大小关系是y1>y2.分析 利用一次函数的增减性判断即可.
解答 解:
在一次函数y=-2x+3中,
∵k=-1<0,
∴y随x的增大而减小,
∵-1<3,
∴y1>y2,
故答案为:y1>y2.
点评 本题主要考查一次函数的增减性,掌握一次函数的增减性是解题的关键,即在y=kx+b中,当k>0时y随x的而增大,当k<0时,y随x的增大而减小.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
17.下列说法正确的是( )
| A. | △ABC的两边长AB=5,AC=12,则BC=13 | |
| B. | Rt△ABC中a=6,b=8,则c=10 | |
| C. | Rt△ABC中a=3,b=4,则△ABC的面积S=6 | |
| D. | 等边△ABC的边长为12,则高AD=6$\sqrt{3}$ |
1. 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0),下列说法:
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0),下列说法:
①b2-4ac=0;
②4a+2b+c<0;
③3a+c=0;
④若(-5,y1),(2,y2)是抛物线上的两点,则y1>y2,
其中正确的是( )
 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0),下列说法:
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0),下列说法:①b2-4ac=0;
②4a+2b+c<0;
③3a+c=0;
④若(-5,y1),(2,y2)是抛物线上的两点,则y1>y2,
其中正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.一次函数y=-x+4的图象与两坐标轴所围成的三角形的面积为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
15. 现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )
现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )
 现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )
现有一张圆心角为108°,半径为4cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为1cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的面积为( )| A. | 0.8πcm2 | B. | 3.2πcm2 | C. | 4πcm2 | D. | 4.8πcm2 |
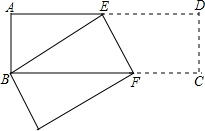 如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为6cm2.
如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为6cm2.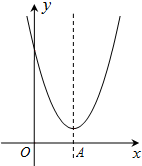 如图,二次函数y=x2-4x+3+$\sqrt{3}$的图象的对称轴交x轴于A点.
如图,二次函数y=x2-4x+3+$\sqrt{3}$的图象的对称轴交x轴于A点. 如图,若A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,若A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=$\frac{m}{x}$的图象的两个交点.