题目内容
5.阅读下面材料:在数学课上,老师提出如下问题:
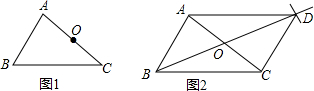
已知:如图1,△ABC及AC边的中点O.
求作:平行四边形ABCD.
小敏的作法如下:
①连接BO并延长,在延长线上截取OD=BO;
②连接DA、DC.所以四边形ABCD就是所求作的平行四边形.
老师说:“小敏的作法正确.”
请回答:小敏的作法正确的理由是对角线互相平分的四边形是平行四边形.
分析 由题意可得OA=OC,OB=OD,然后由对角线互相平分的四边形是平行四边形,证得结论.
解答 解:∵O是AC边的中点,
∴OA=OC,
∵OD=OB,
∴四边形ABCD是平行四边形.
依据:对角线互相平分的四边形是平行四边形.
故答案为:对角线互相平分的四边形是平行四边形.
点评 此题考查了平行四边形的判定.注意掌握对角线互相平分的四边形是平行四边形定理的应用是解此题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
15.下面的调查中,不适合抽样调查的是( )
| A. | 一批炮弹的杀伤力的情况 | B. | 了解一批灯泡的使用寿命 | ||
| C. | 全面人口普查 | D. | 全市学生每天参加体育锻炼的时间 |
10.下列计算正确的是( )
| A. | a5+a5=a10 | B. | (x3)3=x6 | C. | x5•x=x6 | D. | (ab2)3=ab6 |
17.下列说法正确的是( )
| A. | △ABC的两边长AB=5,AC=12,则BC=13 | |
| B. | Rt△ABC中a=6,b=8,则c=10 | |
| C. | Rt△ABC中a=3,b=4,则△ABC的面积S=6 | |
| D. | 等边△ABC的边长为12,则高AD=6$\sqrt{3}$ |
 如图,点P是等边三角形ABC内的一点,连结PB、PC.将△PBC绕点B逆时针旋转到△P′BA的位置,则∠PBP′的度数是60°.
如图,点P是等边三角形ABC内的一点,连结PB、PC.将△PBC绕点B逆时针旋转到△P′BA的位置,则∠PBP′的度数是60°.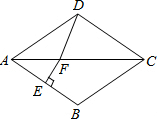 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于60°.
如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于60°.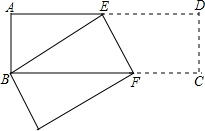 如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为6cm2.
如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为6cm2.