题目内容
2.已知开口向下的抛物线y=ax2+bx+c与x轴交于两点A(x1,0),B(x2,0),其中x1<x2,P为顶点,∠APB=90°,若x1,x2是方程x2-2(m-2)+m2-21=0的两个根,且x12+x22=26.(1)求A,B两点的坐标;
(2)求抛物线的函数关系式.
分析 (1)利用根与系数的关系得到x1+x2=2(m-2),x1•x2=m2-21,再由x12+x22=26得(x1+x2)2-2x1•x2=26,则4(m-2)2-2(m2-21)=26,解得m1=m2=4,所以一元二次方程为x2-4x-5=0,解得x1=-1,x2=5,于是可得到A,B两点的坐标;
(2)作PH⊥x轴于H,如图,利用抛物线的对称性得△PAB为等腰三角形,而∠APB=90°,所以△PAB为等腰直角三角形,根据等腰直角三角形的性质得PH=AH=BH=$\frac{1}{2}$AB=3,则OH=3-1=2,所以P(2,3),然后利用交点式求抛物线解析式.
解答 解:(1)∵x1,x2是方程x2-2(m-2)+m2-21=0的两个根,
∴x1+x2=2(m-2),x1•x2=m2-21,
∵x12+x22=26,
∴(x1+x2)2-2x1•x2=26,
∴4(m-2)2-2(m2-21)=26,
整理得m2-8m+16=0,解得m1=m2=4,
一元二次方程化为x2-4x-5=0,解得x1=-1,x2=5,
∴A(-1,0),B(5,0);
(2)作PH⊥x轴于H,如图,则△PAB为等腰三角形,
∵∠APB=90°,
∴△PAB为等腰直角三角形,
∴PH=AH=BH=$\frac{1}{2}$AB=$\frac{1}{2}$×(5+1)=3,
∴OH=3-1=2,
∴P(2,3),
设抛物线解析式为y=a(x+1)(x-5),
把P(2,3)代入得a•3•(-3)=3,解得a=-$\frac{1}{3}$,
∴抛物线解析式为y=-$\frac{1}{3}$(x+1)(x-5),即y=-$\frac{1}{3}$x2+$\frac{4}{3}$x+$\frac{5}{3}$.
点评 本题考查了抛物线与x轴的交点:从二次函数的交点式y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).也考查了根与系数的关系、待定系数法求抛物线解析式和等腰直角三角形的性质.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案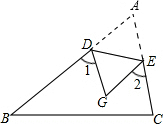 如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )
如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )| A. | 50° | B. | 65° | C. | 100° | D. | 130° |
 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若已知BC=15cm,AC=20cm.求AB和CD的长.
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若已知BC=15cm,AC=20cm.求AB和CD的长.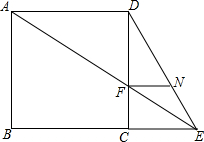 已知:如图,E为正方形ABCD的边BC延长线上的一点,AE交CD于点F,FN∥AD交DE于点N.
已知:如图,E为正方形ABCD的边BC延长线上的一点,AE交CD于点F,FN∥AD交DE于点N. 一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后按图中箭头所示方向跳动 且每秒跳动一个单位,那么第50秒时跳蚤所在位置的坐标是(1,7).
一只跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后按图中箭头所示方向跳动 且每秒跳动一个单位,那么第50秒时跳蚤所在位置的坐标是(1,7).