题目内容
17.若抛物线y=x2+(m2-49)x-m与x轴的两个交点关于y轴对称,则m的值为7.分析 抛物线对称轴为y轴,即对称轴是直线x=0,根据对称轴表达式可列方程求解.
解答 解:根据题意得:$\frac{{m}^{2}-49}{2}$=0,
解得:m=±7(负值不合题意,舍去),
故m=7.
故答案为:7.
点评 本题考查了抛物线与x轴的交点;熟练掌握抛物线与x轴的两个交点关于y轴对称的特点是解决问题的关键.

练习册系列答案
相关题目
5.若抛物线y=x2-4x+4n与x轴只有一个公共点,则n的值为( )
| A. | 4 | B. | -4 | C. | 1 | D. | -1 |
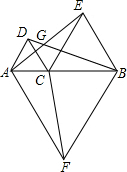 已知:C是AB上的一点,以AC为边作等边△ACD,以BC为边向AD所在的一侧作等边△BCE,以AB为边向AD所在的另一侧作等边△ABF,AE、B0相交于G,连结CF.求证:AE=BD=CF.
已知:C是AB上的一点,以AC为边作等边△ACD,以BC为边向AD所在的一侧作等边△BCE,以AB为边向AD所在的另一侧作等边△ABF,AE、B0相交于G,连结CF.求证:AE=BD=CF. 如图:AB、CD分别是⊙O的直径与弦,且AB⊥CD,∠B=30°,判断△ACD的形状,并说明理由.
如图:AB、CD分别是⊙O的直径与弦,且AB⊥CD,∠B=30°,判断△ACD的形状,并说明理由.