题目内容
12.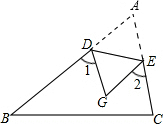 如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )
如图,把△ABC沿DE所在直线折叠,点A落在点C处,若∠A=50°,则∠1+∠2的度数是( )| A. | 50° | B. | 65° | C. | 100° | D. | 130° |
分析 根据三角形内角和定理求出∠AED+∠ADE,根据折叠性质得出∠GED=∠AED,∠GDE=∠ADE,即可求出答案.
解答 解:∵∠A=50°
∴∠AED+∠ADE=180°-∠A=180°-50°=130°,
∵△ABC沿DE所在直线折叠,点A落在点G处,
∴∠GED=∠AED,∠GDE=∠ADE,
∴∠GED+∠GDE=130°,
∴∠1+∠2=360°-(∠GED+∠GDE+∠AED+∠ADE)=100°,
故选C.
点评 本题考查了三角形内角和定理,折叠性质的应用,关键是求出∠AED+∠ADE=∠GED+∠GDE=130°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.若抛物线y=x2-4x+4n与x轴只有一个公共点,则n的值为( )
| A. | 4 | B. | -4 | C. | 1 | D. | -1 |
20.若△ABC≌△DEF,△ABC的周长为100,AB=30,EF=25,则AC=( )
| A. | 55 | B. | 45 | C. | 30 | D. | 25 |
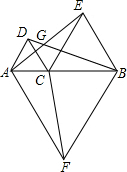 已知:C是AB上的一点,以AC为边作等边△ACD,以BC为边向AD所在的一侧作等边△BCE,以AB为边向AD所在的另一侧作等边△ABF,AE、B0相交于G,连结CF.求证:AE=BD=CF.
已知:C是AB上的一点,以AC为边作等边△ACD,以BC为边向AD所在的一侧作等边△BCE,以AB为边向AD所在的另一侧作等边△ABF,AE、B0相交于G,连结CF.求证:AE=BD=CF.