题目内容
13.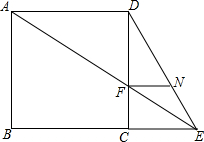 已知:如图,E为正方形ABCD的边BC延长线上的一点,AE交CD于点F,FN∥AD交DE于点N.
已知:如图,E为正方形ABCD的边BC延长线上的一点,AE交CD于点F,FN∥AD交DE于点N.求证:CF=NF.
分析 由四边形ABCD是正方形,可得AB∥CD,AD∥BC,AB=AD,即可证得△CEF∽△BEA,△EFN∽△EAD,然后由相似三角形的对应边成比例,证得结论.
解答 证明:∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,AB=AD,
∴△CEF∽△BEA,△EFN∽△EAD,
∴$\frac{CF}{AB}$=$\frac{EF}{AE}$,$\frac{FN}{AD}$=$\frac{EF}{AE}$,
∴$\frac{FN}{AD}=\frac{CF}{AB}$
∴CF=FN.
点评 此题考查了相似三角形的判定与性质以及正方形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
18.已知方程(x+3)2=5(x+3),则该方程用因式分解法可化简为( )
| A. | (x+3)(x+5)=0 | B. | (x+3)(x+2)=0 | C. | (x+3)(x-5)=0 | D. | (x+3)(x-2)=0 |
5.若抛物线y=x2-4x+4n与x轴只有一个公共点,则n的值为( )
| A. | 4 | B. | -4 | C. | 1 | D. | -1 |
20.若△ABC≌△DEF,△ABC的周长为100,AB=30,EF=25,则AC=( )
| A. | 55 | B. | 45 | C. | 30 | D. | 25 |
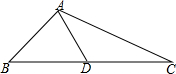 如图,△ABC中,AB=1,AC=$\sqrt{3}$,边BC上的中线AD=$\frac{\sqrt{2}}{2}$,则BC=$\sqrt{6}$.
如图,△ABC中,AB=1,AC=$\sqrt{3}$,边BC上的中线AD=$\frac{\sqrt{2}}{2}$,则BC=$\sqrt{6}$.