题目内容
10.按要求解下列方程(1)配方法:x2-4x-8=0;
(2)因式分解:2(x-3)-5x(x-3)=0.
分析 (1)首先找出方程中a=1,b=-4,c=-8,然后求出根的判别式,进而代入求根公式即可;
(2)首先提取公因式(x-3),进而得到(x-3)(2-5x)=0,再解两个一元一次方程即可.
解答 解:(1)∵a=1,b=-4,c=-8,
∴b2-4ac=16+32=48,
∴x=$\frac{4±\sqrt{48}}{2}$=2±$\sqrt{3}$,
∴x1=2+$\sqrt{3}$,x2=2-$\sqrt{3}$;
(2)∵2(x-3)-5x(x-3)=0,
∴(x-3)(2-5x)=0,
∴x-3=0或2-5x=0,
∴x1=3,x2=$\frac{2}{5}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
2.若a<$\sqrt{20}$<b,其中a,b是两个连续的整数,则a+b=( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
18.已知方程(x+3)2=5(x+3),则该方程用因式分解法可化简为( )
| A. | (x+3)(x+5)=0 | B. | (x+3)(x+2)=0 | C. | (x+3)(x-5)=0 | D. | (x+3)(x-2)=0 |
5.若抛物线y=x2-4x+4n与x轴只有一个公共点,则n的值为( )
| A. | 4 | B. | -4 | C. | 1 | D. | -1 |
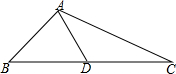 如图,△ABC中,AB=1,AC=$\sqrt{3}$,边BC上的中线AD=$\frac{\sqrt{2}}{2}$,则BC=$\sqrt{6}$.
如图,△ABC中,AB=1,AC=$\sqrt{3}$,边BC上的中线AD=$\frac{\sqrt{2}}{2}$,则BC=$\sqrt{6}$.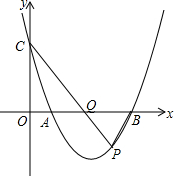 已知抛物线y=$\frac{3}{4}$x2-$\frac{15}{4}$x+3交x轴于A、B点,交y轴于点C,点P为x轴下方抛物线上一点,CP交x轴于点Q,当S△ACQ=S△PBQ,求点P的坐标.
已知抛物线y=$\frac{3}{4}$x2-$\frac{15}{4}$x+3交x轴于A、B点,交y轴于点C,点P为x轴下方抛物线上一点,CP交x轴于点Q,当S△ACQ=S△PBQ,求点P的坐标.