题目内容
13. 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若已知BC=15cm,AC=20cm.求AB和CD的长.
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,若已知BC=15cm,AC=20cm.求AB和CD的长.
分析 由勾股定理求出AB的长,由△ABC的面积=$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC,即可求出CD的长.
解答 解:∵∠ACB=90°,
由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{2{0}^{2}+1{5}^{2}}$=25,
∵△ABC的面积=$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC,
即$\frac{1}{2}$×25×CD=$\frac{1}{2}$×20×15,
解得:CD=12.
点评 本题考查了勾股定理、直角三角形面积的计算方法;熟练掌握勾股定理,运用勾股定理求出AB,再由直角三角形面积的计算方法得出CD是解决问题的关键.

练习册系列答案
相关题目
2.若a<$\sqrt{20}$<b,其中a,b是两个连续的整数,则a+b=( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
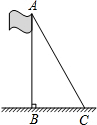 数学综合实验课上,同学们在测量学校旗杆的高度的时候发现:将旗杆顶端升旗用的绳子垂到地面还多2米,当把绳子的下端拉开8米后,下端刚好接触到地面,且绳子处于绷直状态.根据以上数据,计算旗杆的高度和升旗用的绳子的长度.
数学综合实验课上,同学们在测量学校旗杆的高度的时候发现:将旗杆顶端升旗用的绳子垂到地面还多2米,当把绳子的下端拉开8米后,下端刚好接触到地面,且绳子处于绷直状态.根据以上数据,计算旗杆的高度和升旗用的绳子的长度.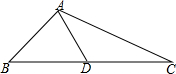 如图,△ABC中,AB=1,AC=$\sqrt{3}$,边BC上的中线AD=$\frac{\sqrt{2}}{2}$,则BC=$\sqrt{6}$.
如图,△ABC中,AB=1,AC=$\sqrt{3}$,边BC上的中线AD=$\frac{\sqrt{2}}{2}$,则BC=$\sqrt{6}$.