题目内容
10.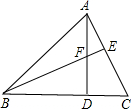 如图,AD是△ABC的边BC上的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD.
如图,AD是△ABC的边BC上的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD.(1)试说明△BDF≌△ADC;
(2)试说明BE⊥AC.
分析 (1)因为AD为△ABC上的高,所以∠ADB=∠ADC=90°,又因为BF=AC,FD=CD,则可根据HL判定△ADC≌△BDF;
(2)因为△ADC≌△BDF,则有∠EBC=∠DAC,又因为∠DAC+∠ACD=90°,所以∠EBC+∠ACD=90°,则BE⊥AC.
解答 证明:(1)∵AD⊥BC,
∴∠ADB=∠ADC=90°.
又∵BF=AC,FD=CD,
∴△ADC≌△BDF(HL);
(2)∵△ADC≌△BDF,
∴∠EBC=∠DAC.
又∵∠DAC+∠ACD=90°,
∴∠EBC+∠ACD=90°.
∴BE⊥AC.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.发现并利用两个直角三角形全等是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
5.已知△ABC≌△DEF,∠A=70°,∠E=50°,则∠F的度数为( )
| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
 如图,已知△ABE≌△ADC,∠1=36°,∠DAE=76°,∠B=25°.求∠DAC、∠C的度数.
如图,已知△ABE≌△ADC,∠1=36°,∠DAE=76°,∠B=25°.求∠DAC、∠C的度数.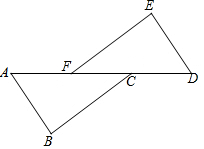 如图所示,已知AF=DC,BC∥EF,AB∥DE,求证:△ABC≌△DEF.
如图所示,已知AF=DC,BC∥EF,AB∥DE,求证:△ABC≌△DEF.