题目内容
2.方程x2-2|3-x|+|x+1|-4=0的解为x=$\frac{-3+3\sqrt{5}}{2}$或x=$\frac{-1-3\sqrt{5}}{2}$.分析 根据方程,运用分类讨论的数学思想可以解答此方程.
解答 解:当x>3时,
x2-2|3-x|+|x+1|-4=0
可化为,x2-2(x-3)+x+1-4=0,
解得此方程无解,
当-1<x≤3时,
方程可化为,x2-2(3-x)+(x+1)-4=0,
解得,${x}_{1}=\frac{-3+3\sqrt{5}}{2}$,x2=$\frac{-3-3\sqrt{5}}{2}$(舍去),
当x≤-1时,
方程可化为:x2-2(3-x)-(x+1)-4=0,
解得,${x}_{1}=\frac{-1-3\sqrt{5}}{2},{x}_{2}=\frac{-1+3\sqrt{5}}{2}$(舍去),
故答案为:x=$\frac{-3+3\sqrt{5}}{2}$或x=$\frac{-1-3\sqrt{5}}{2}$.
点评 本题考查一元二次方程的解,解题的关键是明确一元二次方程的解的计算方法.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
11.化简|3.14-π|=( )
| A. | π-3.14 | B. | 3.14+π | C. | 3.14-π | D. | 0 |
12.观察下表三行数的规律,回答下列问题:
(1)第1行的第四个数a是16;第3行的第六个数b是32;
(2)若第1行的某一列的数为c,则第2行与它同一列的数为c+2;(用含c的式子表示)
(3)已知第n列的三个数的和为1282,若设第1行第n列的数为x,试求x的值.
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | 第6列 | … | |
| 第1行 | -2 | 4 | -8 | a | -32 | 64 | … |
| 第2行 | 0 | 6 | -6 | 18 | -30 | 66 | … |
| 第3行 | -1 | 2 | -4 | 8 | -16 | b | … |
(2)若第1行的某一列的数为c,则第2行与它同一列的数为c+2;(用含c的式子表示)
(3)已知第n列的三个数的和为1282,若设第1行第n列的数为x,试求x的值.
 已知:如图,△ABC的顶点都在⊙O上,点P在⊙O上,且∠APC=∠CPB=60°.求证:△ABC是等边三角形.
已知:如图,△ABC的顶点都在⊙O上,点P在⊙O上,且∠APC=∠CPB=60°.求证:△ABC是等边三角形.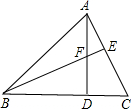 如图,AD是△ABC的边BC上的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD.
如图,AD是△ABC的边BC上的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD. 如图,在△ABC中,AB=AC,∠A=36°,两条角平分线BD、CE相交于点O,则图中全等等腰三角形有3对.
如图,在△ABC中,AB=AC,∠A=36°,两条角平分线BD、CE相交于点O,则图中全等等腰三角形有3对.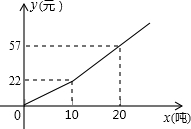 为鼓励市民节约用水,我市自来水公司按分段收费标准收费,右图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.下列结论中:
为鼓励市民节约用水,我市自来水公司按分段收费标准收费,右图反映的是每月收取水费y(元)与用水量x(吨)之间的函数关系.下列结论中: