题目内容
19．
如图，王虎将一块长为4cm，宽为3cm的长方形木板，在桌面上做无滑动的翻滚（顺时针方向）木板上点A位置变化为A→A1→A2，其中第二次翻滚被桌面上一小木块挡住，使木板与桌面成30°角，则点A翻滚到A2位置时共走过的路径长为$\frac{7}{2}$πcm．
分析 点A翻滚到A2位置时，共走过的路径长是二段弧的弧长，第一次的旋转是以B为圆心，AB为半径，旋转的角度是90度，第二次是以C为圆心，AC为半径，旋转的角度是60度，所以根据弧长公式可得．
解答 解：根据弧长公式可得：l=$\frac{90π×5}{180}$+$\frac{60π×3}{180}$=$\frac{7}{2}$π（cm）．
故答案为$\frac{7}{2}$πcm．
点评 本题考查了弧长的计算及矩形的性质，解答本题的关键是找准所旋转的弧的圆心和半径及圆心角的度数，有一定的难度，注意仔细观察．
练习册系列答案
相关题目
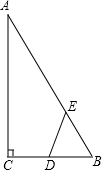如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，D为BC中点．若动点E以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒（0≤t＜6），连接DE，当△BDE是直角三角形时，t的值为2秒或3.5秒或4.5秒．
4．如果一个三角形满足一个角是另一个角的3倍，那么我们称这个三角形为“动感三角形”．下列各组数据中，能作为一个动感三角形三边长的一组是（ ）
| A． | 1，2，3 | B． | 1，1，$\sqrt{2}$ | C． | 1，1，$\sqrt{3}$ | D． | 1，2，$\sqrt{3}$ |
从某个方向观察一个正六棱柱，可看到如图所示的图形，其中四边形ABCD为矩形，E、F分别是AB、DC的中点．若AD=10cm，AB=6cm，则这个正六棱柱的侧面积为120$\sqrt{3}$cm2．