题目内容
8．已知有理数a，b满足a2+4a+2+$\sqrt{b+3}$=-2，求$\sqrt{（2a+b）^{2}}$-$\sqrt{（b-2a）^{2}}$的值．分析 利用配方法和非负数的性质求出a、b，根据二次根式的性质化简，计算即可．
解答 解：∵a2+4a+2+$\sqrt{b+3}$=-2，
∴（a+2）2+$\sqrt{b+3}$=0，
则a+2=0，b+3=0，
解得，a=-2，b=-3，
则$\sqrt{（2a+b）^{2}}$-$\sqrt{（b-2a）^{2}}$=|2a+b|-|b-2a|=|-7|-|1|=6．
点评 本题考查的是二次根式的化简、非负数的性质，掌握二次根式的性质是解题的关键．
练习册系列答案
相关题目
如图，AB=AD，AB⊥AD，AE⊥AC，AE=AC，连接BE，过A作AH⊥CD于H，交BE于F．求证：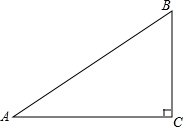
如图，在△ABC中，∠C=90°，AC=8，BC=6，D是AB的中点，点E在边AC上，将△ADE沿DE翻折，使得点A落在点A'处，当A'E⊥AC时，A'B=$\sqrt{2}$或7$\sqrt{2}$．
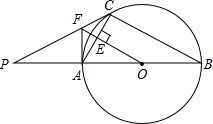如图，C是以AB为直径的⊙O上一点，过O作OE⊥AC于点E，过点A作⊙O的切线交OE的延长线于点F，连接CF并延长交BA的延长线于点P．
8．已知函数f（x）=ax2+2ax+4（0＜a＜3），若x1＜x2，x1+x2=1-a，则（ ）
| A． | f（x1）＜f（x2） | B． | f（x1）=f（x2） | ||
| C． | f（x1）＞f（x2） | D． | f（x1）与f（x2）的大小不能确定 |