题目内容
16.平面直角坐标系内的一条直线同时满足下列两个条件:①不经过第四象限;②与两条坐标轴所围成的三角形的面积为2,这条直线的解析式可以是y=x+2(写出一个解析式即可).分析 设直线解析式为y=kx+b,根据不经过第四象限,与两条坐标轴所围成的三角形的面积为2得出解析式即可.
解答 解:因为不经过第四象限,k>0,b>0,
与两条坐标轴所围成的三角形的面积为2,
可得解析式为y=x+2,
故答案为:y=x+2
点评 本题考查了待定系数法求解析式,关键是根据不经过第四象限,与两条坐标轴所围成的三角形的面积为2解答.

练习册系列答案
相关题目
11.方程组$\left\{\begin{array}{l}{x+3y=7}\\{3x+9y=21}\end{array}\right.$的解的情况是( )
| A. | 无解 | B. | 有一组解 | C. | 有无穷多解 | D. | 不确定 |
1.已知⊙O1与⊙O2的半径分别是2和6,若⊙O1与⊙O2相交,那么圆心距O1O2的取值范围是( )
| A. | 2<O1O2<4 | B. | 2<O1O2<6 | C. | 4<O1O2<8 | D. | 4<O1O2<10 |
16.若角α、β是直角三角形的两个锐角,则$\frac{sinα}{cosβ}$-tan$\frac{α+β}{2}$的值为( )
| A. | 0 | B. | 1 | C. | 1-$\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$-1 |
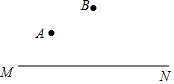 A、B两厂在公路MN同侧,拟在公路边建一货场C,若由B厂独家兴建,并考虑B厂的利益,则要求货场离B厂最近,请在图中作出此时货场C的位置,并说出这样做的道理.
A、B两厂在公路MN同侧,拟在公路边建一货场C,若由B厂独家兴建,并考虑B厂的利益,则要求货场离B厂最近,请在图中作出此时货场C的位置,并说出这样做的道理.