题目内容
3.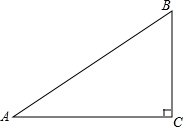 如图,在△ABC中,∠C=90°,AC=8,BC=6,D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使得点A落在点A'处,当A'E⊥AC时,A'B=$\sqrt{2}$或7$\sqrt{2}$.
如图,在△ABC中,∠C=90°,AC=8,BC=6,D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使得点A落在点A'处,当A'E⊥AC时,A'B=$\sqrt{2}$或7$\sqrt{2}$.
分析 分两种情况:
①如图1,作辅助线,构建矩形,先由勾股定理求斜边AB=10,由中点的定义求出AD和BD的长,证明四边形HFGB是矩形,根据同角的三角函数列式可以求DG和DF的长,并由翻折的性质得:∠DA′E=∠A,A′D=AD=5,由矩形性质和勾股定理可以得出结论:A′B=$\sqrt{2}$;
②如图2,作辅助线,构建矩形A′MNF,同理可以求出A′B的长.
解答 解:分两种情况:
①如图1,过D作DG⊥BC与G,交A′E与F,过B作BH⊥A′E与H,
∵D为AB的中点,
∴BD=$\frac{1}{2}$AB=AD,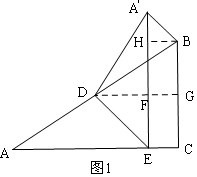
∵∠C=90,AC=8,BC=6,
∴AB=10,
∴BD=AD=5,
sin∠ABC=$\frac{DG}{BD}=\frac{AC}{AB}$,
∴$\frac{DG}{5}=\frac{8}{10}$,
∴DG=4,
由翻折得:∠DA′E=∠A,A′D=AD=5,
∴sin∠DA′E=sin∠A=$\frac{BC}{AB}=\frac{DF}{A′D}$,
∴$\frac{6}{10}=\frac{DF}{5}$,
∴DF=3,
∴FG=4-3=1,
∵A′E⊥AC,BC⊥AC,
∴A′E∥BC,
∴∠HFG+∠DGB=180°,
∵∠DGB=90°,
∴∠HFG=90°,
∵∠EHB=90°,
∴四边形HFGB是矩形,
∴BH=FG=1,
同理得:A′E=AE=8-1=7,
∴A′H=A′E-EH=7-6=1,
在Rt△AHB中,由勾股定理得:A′B=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$;
②如图2,过D作MN∥AC,交BC与于N,过A′作A′F∥AC,交BC的延长线于F,延长A′E交直线DN于M,
∵A′E⊥AC,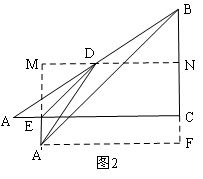
∴A′M⊥MN,A′E⊥A′F,
∴∠M=∠MA′F=90°,
∵∠ACB=90°,
∴∠F=∠ACB=90°,
∴四边形MA′FN是矩形,
∴MN=A′F,FN=A′M,
由翻折得:A′D=AD=5,
Rt△A′MD中,∴DM=3,A′M=4,
∴FN=A′M=4,
Rt△BDN中,∵BD=5,
∴DN=4,BN=3,
∴A′F=MN=DM+DN=3+4=7,
BF=BN+FN=3+4=7,
Rt△ABF中,由勾股定理得:A′B=$\sqrt{{7}^{2}+{7}^{2}}$=7$\sqrt{2}$;
综上所述,A′B的长为$\sqrt{2}$或7$\sqrt{2}$.
故答案为:$\sqrt{2}$或7$\sqrt{2}$.
点评 本题考查了翻折变换的性质、勾股定理、矩形的性质、三角函数及解直角三角形的有关知识,作辅助线构建矩形是本题的关键,明确翻折前后的对应角和边相等,在证明中利用同角的三角函数列比例式比证明相似列比例式计算简单.

 阅读快车系列答案
阅读快车系列答案| 柑橘总质量n/Kg | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
| 损坏柑橘质量m/Kg | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.51 |
| 柑橘损坏的频率$\frac{m}{n}$ (结果保留小数点后三位) | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
| A. | 无解 | B. | 有一组解 | C. | 有无穷多解 | D. | 不确定 |
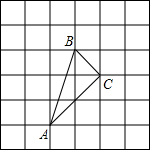 如图,小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点处,判断△ABC的形状,并求出△ABC的面积.
如图,小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点处,判断△ABC的形状,并求出△ABC的面积.