题目内容
4. 如图,在△ABC中,GD⊥AC于点D,∠AFE=∠ABC,∠1+∠2=180°,∠AEF=65°.求:∠1的度数.
如图,在△ABC中,GD⊥AC于点D,∠AFE=∠ABC,∠1+∠2=180°,∠AEF=65°.求:∠1的度数.
分析 根据平行线的判定得到EF∥BC,由平行线的性质得到∠1=∠EBG,等量代换得到∠EBG+∠2=180°,于是得到EB∥DG,根据平行线的性质得到∠GDE=∠BEA,由垂直的定义得到∠GDE=90°,即可的结论.
解答 解:∵∠AFE=∠ABC,
∴EF∥BC,
∴∠1=∠EBG,
∵∠1+∠2=180°,
∴∠EBG+∠2=180°,
∴EB∥DG,
∴∠GDE=∠BEA,
∵GD⊥AC于点D,
∴∠GDE=90°,
∴∠BEA=∠GDE=90°,
∴∠1=∠BEA-∠AEF=90°-65°=25°.
点评 本题考查了平行线的判定和性质,垂直的定义,熟练掌握平行线的判定定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 某公司欲招聘职员一名,对甲乙丙三名候选人进行了笔试和面试两项测试,其成绩如表所示:根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票得2分(没有弃权票,每人只能1投票)
某公司欲招聘职员一名,对甲乙丙三名候选人进行了笔试和面试两项测试,其成绩如表所示:根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票得2分(没有弃权票,每人只能1投票)
(1)请算出三人的民主评议得分;
(2)该单位将笔试,面试,民主评议三项测试得分按2:1:2的比例确定综合成绩,谁将被录用?请说明理由.
 某公司欲招聘职员一名,对甲乙丙三名候选人进行了笔试和面试两项测试,其成绩如表所示:根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票得2分(没有弃权票,每人只能1投票)
某公司欲招聘职员一名,对甲乙丙三名候选人进行了笔试和面试两项测试,其成绩如表所示:根据录用程序,该单位又组织了100名评议人员对三人进行投票测评,其得票率如扇形图所示,每票得2分(没有弃权票,每人只能1投票)| 测试项目 | 测试成绩分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 80 | 85 | 95 |
| 面试 | 98 | 75 | 73 |
(2)该单位将笔试,面试,民主评议三项测试得分按2:1:2的比例确定综合成绩,谁将被录用?请说明理由.
9.下列实数中,无理数是( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | 3.$\stackrel{•}{1}$$\stackrel{•}{4}$ | D. | $\sqrt{3}$ |
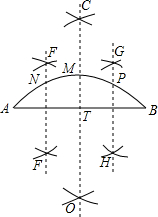 小明四等分弧AB,他的作法如下:
小明四等分弧AB,他的作法如下: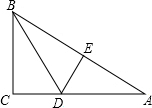 如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE.
如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE. 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{7}{2}$x与矩形OABC的边AB交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为( )
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{7}{2}$x与矩形OABC的边AB交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为( )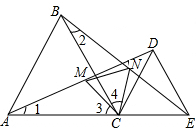 如图,已知点A、C、E在同一直线上,△ABC和△CDE都是等边三角形,M、N分别为AD、BE的中点,求证:△CMN是等边三角形.
如图,已知点A、C、E在同一直线上,△ABC和△CDE都是等边三角形,M、N分别为AD、BE的中点,求证:△CMN是等边三角形.